题目内容
19.在平面直角坐标系xOy中,向量$\overrightarrow{OA}$=(0,3),向量$\overrightarrow{OB}$=(4,3),若已知向量$\overrightarrow{OC}$=λ$\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}$+$\frac{\overrightarrow{OB}}{|\overrightarrow{OB}|}$(λ∈R,λ>0),则|$\overrightarrow{OC}$|=$\sqrt{5}$,则C点的坐标为($\frac{4}{5}$,$\frac{\sqrt{109}}{5}$).分析 先根据向量$\overrightarrow{OA},\overrightarrow{OB}$的坐标,求出$|\overrightarrow{OA}|=3,|\overrightarrow{OB}|=5$,从而得到$\overrightarrow{OC}=(\frac{4}{5},λ+\frac{3}{5})$,根据向量长度$|\overrightarrow{OC}|=\sqrt{5}$,即可得到$5=(\frac{4}{5})^{2}+(λ+\frac{3}{5})^{2}$,解该方程,并取λ>0解,这样即可得出$\overrightarrow{OC}$的坐标,从而得出点C的坐标.
解答 解:根据条件,$|\overrightarrow{OA}|=3,|\overrightarrow{OB}|=5$;
∴$\overrightarrow{OC}=\frac{λ}{3}•(0,3)+\frac{1}{5}•(4,3)=(\frac{4}{5},λ+\frac{3}{5})$;
又$|\overrightarrow{OC}|=\sqrt{5}$;
∴${\overrightarrow{OC}}^{2}=\frac{16}{25}+{λ}^{2}+\frac{6}{5}λ+\frac{9}{25}=5$;
解得$λ=\frac{-3±\sqrt{109}}{5}$;
∵λ>0;
∴$λ=\frac{-3+\sqrt{109}}{5}$;
∴$\overrightarrow{OC}=(\frac{4}{5},\frac{\sqrt{109}}{5})$;
∴C点的坐标为($\frac{4}{5},\frac{\sqrt{109}}{5}$).
故答案为:($\frac{4}{5}$,$\frac{\sqrt{109}}{5}$).
点评 考查根据向量的坐标求向量的长度,向量坐标的数乘即加法运算,数量积的坐标运算,以及解一元二次方程,清楚向量坐标和对应点的坐标的关系.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案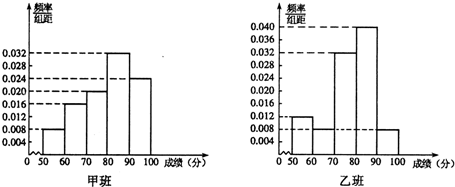
(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(1)若甲、乙、丙三支足球队实力相当,每两支球队比赛时,胜、平、负的概率均为$\frac{1}{3}$,
求甲队能保持不败的概率
(2)若甲、乙两队实力相当,且优于丙,具体数据如下表
若获胜一场积3分,平一场积1分,输一场积0分,记X表示甲队的积分,求X的分布列和数学期望
| 概率 事件 | 甲胜乙 | 甲平乙 | 甲输乙 |
| 概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
| 概率 事件 | 甲胜丙 | 甲平丙 | 甲输丙 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
| 概率 事件 | 乙胜丙 | 乙平丙 | 乙输丙 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |