题目内容
10．已知关于x的一元二次方程（x-1）（3-x）=a-x（a∈R），试讨论方程实数根的个数．分析 方程可化为x2-5x+a+3=0，利用判别式，即可讨论方程实数根的个数．
解答 解：方程可化为x2-5x+a+3=0
△=52-4（a+3）=25-4a-12=13-4a
当△＞0，即a＜$\frac{13}{4}$时，方程有两个不相等的实数根；
当△=0，即a=$\frac{13}{4}$时，方程有两个相等的实数根；
当△＜0，即a＞$\frac{13}{4}$时，方程没有实数根．
点评 本题考查讨论方程实数根的个数，考查学生的计算能力，属于中档题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
20．若f（x）是定义在R上的偶函数，且满足f（x）=-f（x+$\frac{3}{2}$），f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2008）的值为（ ）
| A． | -2 | B． | 0 | C． | 1 | D． | 2 |
1．函数y=$\frac{{x}^{2}+2x+6}{x-1}$（x＞1）的最小值为（ ）
| A． | 10 | B． | 9 | C． | 6 | D． | 4 |
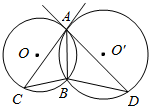如图，⊙O和⊙O′都经过A，B两点，AC是⊙O′的切线，交⊙O于点C，AD是⊙O的切线，交⊙O′于点D，若BC=2，BD=6，则AB的长为2$\sqrt{3}$．