18.函数f(x)=ex+x2+2x+1与g(x)的图象关于直线3x-y-2=0对称,P,Q分别是函数f(x),g(x)图象上的动点,则|PQ|的最小值为( )
| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{6\sqrt{10}}{10}$ | D. | $\frac{4\sqrt{10}}{5}$ |
17.f(x)=-$\frac{1}{2}$x2+bln(x+2)在(-1,+∞)上单调递减,则b的取值范围是( )
| A. | (-∞,-1) | B. | (-1,+∞) | C. | [-1,+∞) | D. | (-∞,-1] |
14.为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
(Ⅰ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段居民的休闲方式与性别有关系”?
(Ⅱ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X.求X的数学期望和方差.
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$.
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(Ⅱ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X.求X的数学期望和方差.
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
9.某学校要从5名男生和2名女生中选出3人作为志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ等于( )
0 247030 247038 247044 247048 247054 247056 247060 247066 247068 247074 247080 247084 247086 247090 247096 247098 247104 247108 247110 247114 247116 247120 247122 247124 247125 247126 247128 247129 247130 247132 247134 247138 247140 247144 247146 247150 247156 247158 247164 247168 247170 247174 247180 247186 247188 247194 247198 247200 247206 247210 247216 247224 266669
| A. | $\frac{4}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{6}{7}$ | D. | 1 |
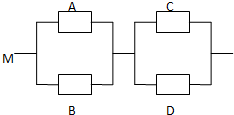 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.