19.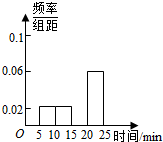 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)求旅客购票用时的平均数
(4)若每增加一个购票窗口可使平均购票用时缩短5min,要使平均购票用时不超过10min,那么你估计最少要增加几个窗口?
 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合计 | 100 | 1.00 | |
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)求旅客购票用时的平均数
(4)若每增加一个购票窗口可使平均购票用时缩短5min,要使平均购票用时不超过10min,那么你估计最少要增加几个窗口?
16.复数(3-4i)i(其中i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.设甲,乙两个圆柱的底面面积分别为S1,S2,体积为V1,V2,若它们的侧面积相等且$\frac{S_1}{S_2}=\frac{9}{4}$,则$\frac{V_1}{V_2}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{9}{4}$ |
13.已知圆锥的表面积为6π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}+1$ |
12.(1)在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(I)求回归直线方程$\stackrel{∧}{y}$=bx+a,其中b=-20,a=$\stackrel{∧}{y}$-b$\overline{x}$
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
0 224257 224265 224271 224275 224281 224283 224287 224293 224295 224301 224307 224311 224313 224317 224323 224325 224331 224335 224337 224341 224343 224347 224349 224351 224352 224353 224355 224356 224357 224359 224361 224365 224367 224371 224373 224377 224383 224385 224391 224395 224397 224401 224407 224413 224415 224421 224425 224427 224433 224437 224443 224451 266669
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
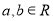 ,则“
,则“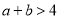 ”是“
”是“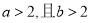 ”的( )
”的( )