0 220748 220756 220762 220766 220772 220774 220778 220784 220786 220792 220798 220802 220804 220808 220814 220816 220822 220826 220828 220832 220834 220838 220840 220842 220843 220844 220846 220847 220848 220850 220852 220856 220858 220862 220864 220868 220874 220876 220882 220886 220888 220892 220898 220904 220906 220912 220916 220918 220924 220928 220934 220942 266669
 ,若存在
,若存在 使得函数
使得函数 的值域为
的值域为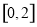 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
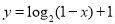 在
在 上是减函数,所以
上是减函数,所以 ,由函数
,由函数 ,解得
,解得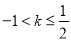 .令
.令 ,则
,则 =
= ,知
,知 在
在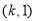 上为减函数,在
上为减函数,在 为增函数.又由
为增函数.又由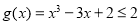 ,得
,得 ,且
,且 ,则必有
,则必有 .如图所示.易知
.如图所示.易知 .
.
 的取值范围也不能得到正确的结果,因此解答本题的关键是求出
的取值范围也不能得到正确的结果,因此解答本题的关键是求出 .
. .
. ,求出实数
,求出实数 的值;
的值; 命题
命题 且
且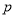 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.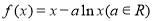 .
.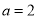 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; ,求函数
,求函数 的单调区间.
的单调区间. ;(2)当
;(2)当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增;当
上单调递增;当 时,
时, 在
在 上单调递增.
上单调递增. ,从而问题解决;(2)先求出导函数
,从而问题解决;(2)先求出导函数 ,根据
,根据 求得的区间是单调增区间,
求得的区间是单调增区间,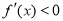 求得的区间是单调减区间,因为在函数式中含字母系数
求得的区间是单调减区间,因为在函数式中含字母系数 ,要对
,要对 时,
时, ,
, ,切点
,切点 ,
, ,∴
,∴ ,
, 在点
在点 处的切线方程为:
处的切线方程为: ,即
,即 ,定义域为
,定义域为 ,
, ,即
,即 时,令
时,令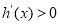 ,
, ,∴
,∴ ,
,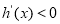 ,∵
,∵ .
. ,即
,即 时,
时, 恒成立,
恒成立,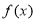 的定义域,利用不等式
的定义域,利用不等式 的解集与定义域的交集为函数的单调递增区间,
的解集与定义域的交集为函数的单调递增区间, 的解集与定义域的交集为函数的单调递减区间;若已知函数在某区间
的解集与定义域的交集为函数的单调递减区间;若已知函数在某区间 上单调递增(减),则转化为不等式
上单调递增(减),则转化为不等式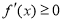 (
( )在区间
)在区间 和
和 ,离心率
,离心率 .
. 与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值. 为一条直线,
为一条直线, 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )
 则
则


 所在平面上有三点
所在平面上有三点 ,满足
,满足 ,
, ,
, ,则
,则 的面积与
的面积与 B.
B. C.
C. D.
D.
 ,
, 是数列
是数列 项和,且满足
项和,且满足 ,则数列
,则数列 _______,通项
_______,通项 _____.
_____. 、
、 、
、 满足
满足 ,
, ,则
,则 的最大值为 .
的最大值为 .
 =( )
=( ) ,
, 是过顶点
是过顶点 圆上的一点,
圆上的一点, 为
为 中点,则
中点,则 与面
与面 所成角余弦值的取值范围是( )
所成角余弦值的取值范围是( ) B.
B. C.
C. D.
D.
 与
与 的关系式为__ ___,
的关系式为__ ___, 的最小值是___ ___.
的最小值是___ ___.