(本小题满分14分)已知曲线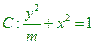 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,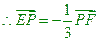 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为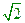 ,且过点
,且过点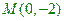 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又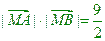 ,求曲线C的方程。
,求曲线C的方程。

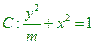 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,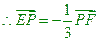 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为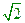 ,且过点
,且过点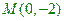 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又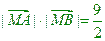 ,求曲线C的方程。
,求曲线C的方程。 
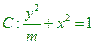 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,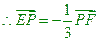 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为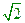 ,且过点
,且过点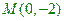 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又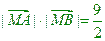 ,求曲线C的方程。
,求曲线C的方程。 