(本小题满分12分)
在平面直角坐标系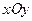 中,已知动点
中,已知动点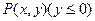 到点
到点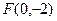 的距离为
的距离为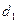 ,到
,到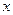 轴的距离为
轴的距离为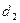 ,且
,且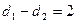 .
.
(I)求点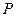 的轨迹
的轨迹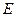 的方程;
的方程;
(Ⅱ)若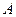 、
、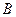 是(I)中
是(I)中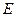 上的两点,
上的两点,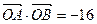 ,过
,过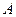 、
、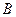 分别作直线
分别作直线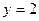 的垂线,垂足分别为
的垂线,垂足分别为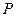 、
、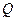 .证明:直线
.证明:直线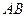 过定点
过定点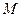 ,且
,且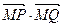 为定值.
为定值.
在平面直角坐标系
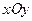 中,已知动点
中,已知动点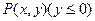 到点
到点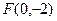 的距离为
的距离为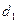 ,到
,到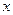 轴的距离为
轴的距离为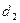 ,且
,且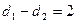 .
.(I)求点
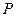 的轨迹
的轨迹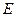 的方程;
的方程;(Ⅱ)若
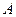 、
、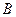 是(I)中
是(I)中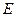 上的两点,
上的两点,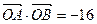 ,过
,过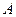 、
、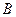 分别作直线
分别作直线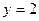 的垂线,垂足分别为
的垂线,垂足分别为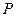 、
、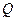 .证明:直线
.证明:直线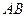 过定点
过定点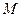 ,且
,且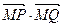 为定值.
为定值.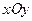 中,已知动点
中,已知动点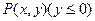 到点
到点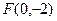 的距离为
的距离为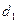 ,到
,到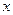 轴的距离为
轴的距离为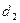 ,且
,且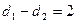 .
.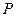 的轨迹
的轨迹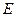 的方程;
的方程;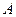 、
、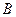 是(I)中
是(I)中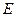 上的两点,
上的两点,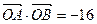 ,过
,过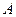 、
、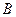 分别作直线
分别作直线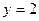 的垂线,垂足分别为
的垂线,垂足分别为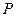 、
、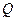 .证明:直线
.证明:直线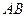 过定点
过定点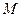 ,且
,且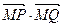 为定值.
为定值.