若直角坐标平面内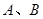 两点满足条件:①点
两点满足条件:①点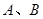 都在
都在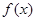 的图象上;②点
的图象上;②点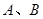 关于原点对称,则对称点对
关于原点对称,则对称点对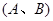 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对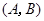 与
与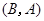 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数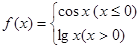 , 则
, 则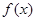 的“兄弟点对”的个数为( )
的“兄弟点对”的个数为( )
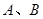 两点满足条件:①点
两点满足条件:①点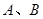 都在
都在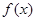 的图象上;②点
的图象上;②点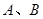 关于原点对称,则对称点对
关于原点对称,则对称点对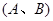 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对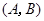 与
与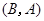 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数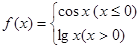 , 则
, 则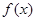 的“兄弟点对”的个数为( )
的“兄弟点对”的个数为( )| A.2 | B.3 | C.4 | D.5 |
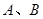 两点满足条件:①点
两点满足条件:①点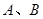 都在
都在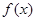 的图象上;②点
的图象上;②点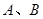 关于原点对称,则对称点对
关于原点对称,则对称点对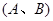 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对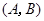 与
与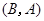 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数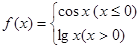 , 则
, 则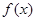 的“兄弟点对”的个数为( )
的“兄弟点对”的个数为( )| A.2 | B.3 | C.4 | D.5 |