题目内容
已知函数 (
( ).
).
(1)证明:当 时,
时,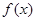 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时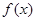 的单调区间;
的单调区间;
(2)已知函数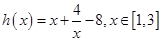 ,函数
,函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 (
( ).
).(1)证明:当
 时,
时,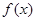 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时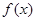 的单调区间;
的单调区间;(2)已知函数
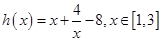 ,函数
,函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)证明详见解析,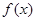 在
在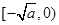 是减函数,在
是减函数,在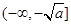 是增函数;(2)
是增函数;(2)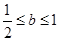 .
.
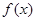 在
在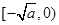 是减函数,在
是减函数,在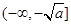 是增函数;(2)
是增函数;(2)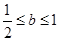 .
.试题分析:(1)根据函数单调性的定义进行证明即①设
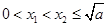 ;②作差:
;②作差: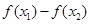 ;③因式分解到最简
;③因式分解到最简 ;④根据条件判定符号;⑤作出结论,经过这五步即可证明
;④根据条件判定符号;⑤作出结论,经过这五步即可证明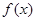 在
在 单调递减,同理可证
单调递减,同理可证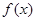 在
在 是增函数,最后由奇函数的性质得出;
是增函数,最后由奇函数的性质得出;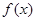 在
在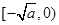 是减函数,在
是减函数,在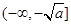 是增函数;(2)先将“对任意
是增函数;(2)先将“对任意 ,总存在
,总存在 ,使得
,使得 成立”转化为“函数
成立”转化为“函数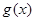 在区间
在区间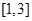 的值域包含了
的值域包含了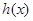 在区间
在区间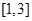 的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到
的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到 的取值范围.
的取值范围.试题解析:(1)证明:当
 时
时①设
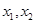 是区间
是区间 上的任意两个实数,且
上的任意两个实数,且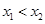 ,则
,则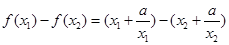

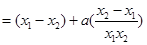

∵
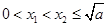 ,∴
,∴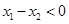 ,
,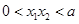
∴
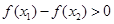 ,即
,即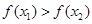
∴
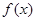 在
在 是减函数 4分
是减函数 4分②同理可证
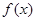 在
在 是增函数 5分
是增函数 5分综上所述得:当
 时,
时, 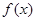 在
在 是减函数,在
是减函数,在 是增函数 6分
是增函数 6分∵函数
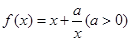 是奇函数,根据奇函数图像的性质可得
是奇函数,根据奇函数图像的性质可得当
 时,
时,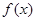 在
在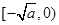 是减函数,在
是减函数,在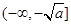 是增函数 8分
是增函数 8分(2)∵
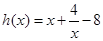 (
(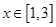 ) 8分
) 8分由(1)知:
 在
在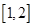 单调递减,
单调递减,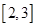 单调递增
单调递增∴
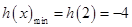
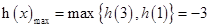 ,
, 10分
10分又∵
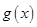 在
在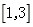 单调递减
单调递减∴由题意知:
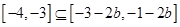
于是有:
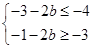 ,解得
,解得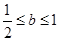 12分.
12分.
练习册系列答案
相关题目
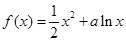 (
(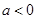 ).
).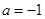 ,求函数
,求函数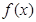 的极值;
的极值;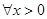 ,不等式
,不等式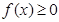 恒成立,求实数
恒成立,求实数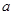 的取值范围.
的取值范围. 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
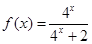
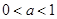 ,求
,求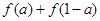 的值;
的值;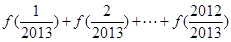 的值.
的值. ,若
,若 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )



 是增函数的是
是增函数的是



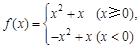 ,则不等式
,则不等式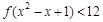 的解集是 .
的解集是 .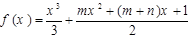 的两个极值点分别为
的两个极值点分别为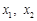 ,且
,且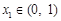 ,
,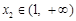 ,点
,点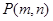 表示的平面区域为
表示的平面区域为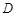 ,若函数
,若函数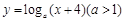 的图像上存在区域
的图像上存在区域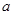 的取值范围是( )
的取值范围是( )


