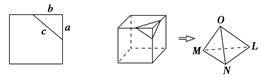
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设 ,正确顺序的序号为
,正确顺序的序号为
| A.①②③ | B.③①② | C.①③② | D.②③① |
观察式子:1+ <
< ,1+
,1+ +
+ <
< ,1+
,1+ +
+ +
+ <
< , ,则可归纳出一般式子为( )
, ,则可归纳出一般式子为( )
A.1+ + + + + + + < < (n≥2) (n≥2) | B.1+ + + + + + + < < (n≥2) (n≥2) |
C.1+ + + + + + + < < (n≥2) (n≥2) | D.1+ + + + + + + < < (n≥2) (n≥2) |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线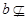 平面
平面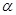 ,直线
,直线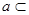 平面
平面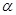 ,直线
,直线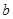 ∥平面
∥平面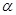 ,则直线
,则直线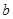 ∥直线
∥直线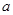 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
用数学归纳法证明不等式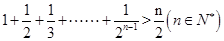 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )
A.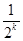 | B.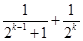 |
C.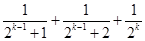 | D. |
(推理)三角形的内角和为180º,凸四边形内角和为360º,那么凸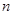 边形的内角和为
边形的内角和为
A.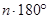 | B.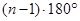 | C.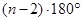 | D.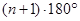 |
(推理)三段论:“①只有船准时起航,才能准时到达目的港;②这艘船是准时到达目的港;③所以这艘船是准时起航的”中的“小前提”是( )
| A.① | B.② | C.①② | D.③ |
下列表述正确的是
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ | C.②④⑤ | D.①③⑤ |
下列平面图形中与空间的平行六面体作为类比对象较合适的是( )
| A.三角形 | B.梯形 | C.平行四边形 | D.矩形 |
下列推理合理的是( )
A.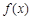 是增函数,则 是增函数,则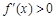 |
B.因为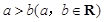 ,则 ,则 |
C.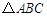 为锐角三角形,则 为锐角三角形,则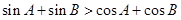 |
D.直线 ,则 ,则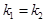 |
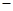 LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .