题目内容
在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2。设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 . 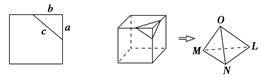
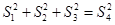
解析试题分析:根据题意,由于在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2,正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,类比得到的结论边推广到面积,在可知为
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,类比得到的结论边推广到面积,在可知为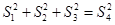 。
。
考点:类比推理
点评:主要是考查了类比推理的运用,属于中档题。

练习册系列答案
相关题目
由“正三角形的内切圆切于三边的中点”可类比猜想:正四面体的内切球切于四个面( )
| A.各正三角形内一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
用数学归纳法证明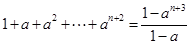 (
(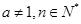 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为
| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
数学归纳法适用于证明的命题类型是
A.已知 结论 结论 | B.结论 已知 已知 | C.直接证明比较困难 | D.与正整数有关 |
用数学归纳法证明不等式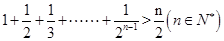 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )
A.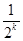 | B.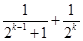 |
C.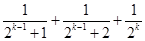 | D. |
观察下列各式: =3125,
=3125, =15625,
=15625, =78125, ,则
=78125, ,则 的末四位数字为( )
的末四位数字为( )
| A.3125 | B.5625 | C.0625 | D.8125 |
有一段演绎推理是这样的,“有些有理数是分数,整数是有理数,则整数是分数”,结论显然是错误的,因为
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
设Sk= +
+ +
+ +…+
+…+ ,则Sk+1=( )
,则Sk+1=( )
A.Sk+ |
B.Sk+ + + |
C.Sk+ - - |
D.Sk+ - - |


