已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
| A.n=k+1时命题成立 |
| B.n=k+2时命题成立 |
| C.n=2k+2时命题成立 |
| D.n=2(k+2)时命题成立 |
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
| A.n=1时成立 | B.n=2时成立 |
| C.n=3时成立 | D.n=4时成立 |
下列表述正确的是 ( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ |
| C.②④⑤ | D.①③⑤ |
观察下列各式:55=3 125,56=15 625,57=78 125,…,则52 011
的末四位数字为 ( ).
| A.3 125 | B.5 625 |
| C.0 625 | D.8 125 |
由集合{a1},{a1,a2},{a1,a2,a3},…的子集个数归纳出集合{a1,
a2,a3,…,an}的子集个数为( )
| A.n | B.n+1 |
| C.2n | D.2n-1 |
下面几种推理过程是演绎推理的是( )
| A.某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人 |
| B.由三角形的性质,推测空间四面体的性质 |
| C.平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 |
D.在数列{an}中,a1=1,an=  ,由此归纳出{an}的通项公式 ,由此归纳出{an}的通项公式 |
定义平面向量之间的一种运算“☉”如下:对任意的a=(m,n),b=(p,q),令a☉b=mq-np.下面说法错误的是( )
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |
在集合{a,b,c,d}上定义两种运算⊕和?如下:
那么d?(a⊕c)等于( )
| A.a | B.b | C.c | D.d |
 =c+d
=c+d (n≥2),每个数是它下一行左右相邻两数的和,如
(n≥2),每个数是它下一行左右相邻两数的和,如 =
=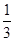 +
+ ,
, +
+ ,则第10行第4个数(从左往右数)为( )
,则第10行第4个数(从左往右数)为( )



