天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的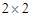 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为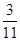 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
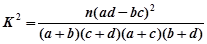 。
。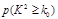 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
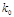 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
根据以上数据建立一个2×2的列联表;
能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据: ,其中
,其中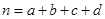 .
.
| K2≥k0 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示
| | 积极参加班级工作 | 不太主动参加班级工作 |
| 学习积极性高 | 18 | 7 |
| 学习积极性一般 | 6 | 19 |
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由
附:
P(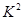 ≥k) ≥k) | 0.050 | 0.010 | 0.001 | 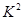 = =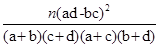 |
| k | 3.841 | 6.635 | 10.828 |
某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1~50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
(Ⅰ)观察乙抽取的样本数据,若从男同学中抽取两名,求两名男同学中恰有一名非优秀的概率.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
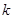 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
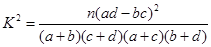 ,其中
,其中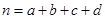 )
) 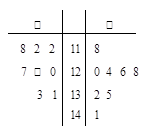
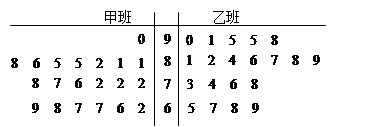

 [(x1-
[(x1- )2+(x2-
)2+(x2- 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图: ,求
,求 .
.

 ,第二类在
,第二类在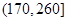 ,第三类在
,第三类在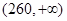 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 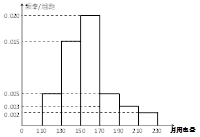
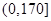 ,第二类在
,第二类在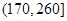 ,第三类在
,第三类在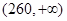 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 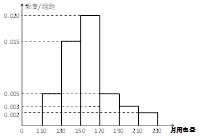
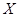 为获奖户数,求
为获奖户数,求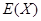 与方差
与方差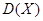 .
.