题目内容
某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示
| | 积极参加班级工作 | 不太主动参加班级工作 |
| 学习积极性高 | 18 | 7 |
| 学习积极性一般 | 6 | 19 |
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由
附:
P(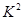 ≥k) ≥k) | 0.050 | 0.010 | 0.001 | 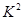 = =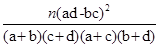 |
| k | 3.841 | 6.635 | 10.828 |
(I)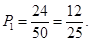 ,
,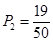 (II)有关系
(II)有关系
解析试题分析:解:⑴随机抽查这个班的一名学生,共有50种不同的抽查方法,
其中积极参加班级工作的学生有18+6=24人,即有24种不同的抽法,
由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是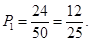
同理可得,抽到不太主动参加班级工作且学习积极性一般的概率是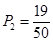 .
.
⑵由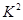 统计量的计算公式得:
统计量的计算公式得: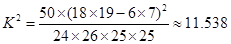 ,
,
由于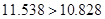 ,所以有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关系”.
,所以有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关系”.
考点:独立性检验的应用.
点评:本题考查独立性检验的应用和等可能事件的概率,本题解题的关键是正确利用观测值公式求出观测值,正确理解临界值对应的概率的意义.

 阅读快车系列答案
阅读快车系列答案某社团组织 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| | 宣传慰问 | 义工 | 总计 |
 岁至 岁至 岁 岁 |  |  |  |
大于 岁 岁 |  | 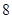 | 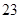 |
| 总计 |  |  |  |
 名,年龄大于
名,年龄大于 岁的应该抽取几名?
岁的应该抽取几名?(2)上述抽取的
 名志愿者中任取
名志愿者中任取 名,求选到的志愿者年龄大于
名,求选到的志愿者年龄大于 岁的人数的数学期望.
岁的人数的数学期望. 某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份样品中,求至多有一份得分在
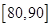 之间的概率.
之间的概率. 某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1~50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
(Ⅰ)观察乙抽取的样本数据,若从男同学中抽取两名,求两名男同学中恰有一名非优秀的概率.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
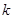 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
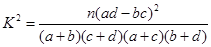 ,其中
,其中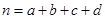 )
) 某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
| | 高一年级 | 高二年级 | 高三年级 |
| 跑步 |  | 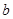 | 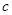 |
| 跳绳 |  |  | 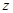 |
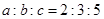 ,全校参与跳绳的人数占总人数的
,全校参与跳绳的人数占总人数的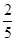 ,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人.
,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
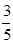 .
.(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
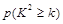 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
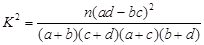 ,其中
,其中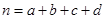 )
)
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | | |
| 不爱好 | | 30 | |
| 总计 | | | |
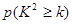 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
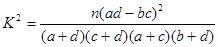
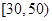 和
和 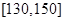 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在
 是月用水量为[0,2)的家庭代表.
是月用水量为[0,2)的家庭代表. 是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表
是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表