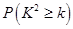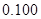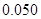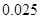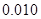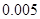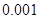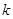我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图: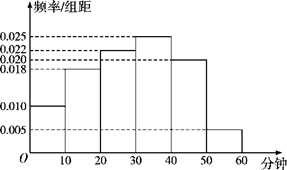
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
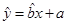 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
某学校高一年学生在某次数学单元测试中,成绩在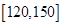 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 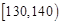 | 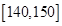 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,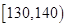 和
和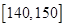 的同学中共抽取
的同学中共抽取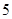 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
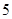 人中,任取
人中,任取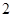 人,求成绩在
人,求成绩在 和
和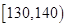 中各有
中各有 人的概率?
人的概率? 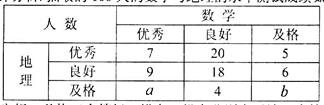
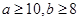 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率. 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
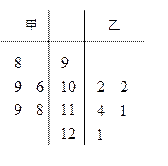


 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率;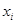 (年)与所支出的维修费
(年)与所支出的维修费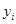 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,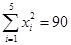 ,
,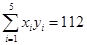 ,
,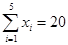 ,
,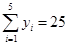 .
.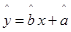 ;
;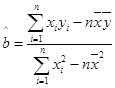 ,
,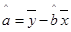 ,其中
,其中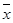 ,
, 为样本平均值.)
为样本平均值.)
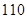 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的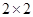 列联表,如表2.
列联表,如表2.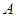 、
、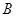 、
、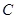 、
、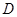 、
、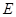 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关; 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.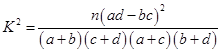 ,其中
,其中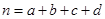 .
.