题目内容
2013年11月,青岛发生输油管道爆炸事故造成胶州湾局部污染.国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作,有关数据见表1(单位:人)
海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响,随机选取了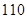 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的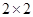 列联表,如表2.
列联表,如表2.
(1)求研究小组的总人数;
(2)写出表2中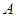 、
、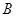 、
、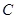 、
、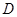 、
、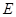 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
(3)若从研究小组的环保专家和海洋生物专家中随机选 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.
附:①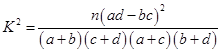 ,其中
,其中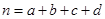 .
.
②
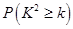 | 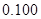 | 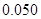 | 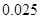 | 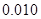 | 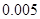 | 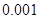 |
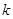 | 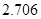 | 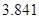 | 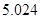 | 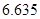 |  | 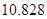 |
(1) ;(2)
;(2) ,
,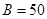 ,
,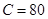 ,
,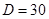 ,
,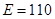 ,
,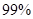 ;(3)
;(3)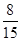 .
.
解析试题分析:(1)先根据分层抽样列方程求出 和
和 的值,从而求出所抽取的总人数;(2)根据表中数据求出
的值,从而求出所抽取的总人数;(2)根据表中数据求出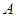 、
、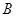 、
、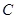 、
、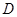 、
、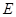 的值,然后根据独立性检验的基本思想求出犯错误的概率,从而得到相关性的把握;(3)利用列举法求出所有的基本事件数以及问题中涉及的事件所包含的基本事件数,最后利用古典概型的概率计算公式求出相应事件的概率.
的值,然后根据独立性检验的基本思想求出犯错误的概率,从而得到相关性的把握;(3)利用列举法求出所有的基本事件数以及问题中涉及的事件所包含的基本事件数,最后利用古典概型的概率计算公式求出相应事件的概率.
(1)由题意知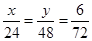 ,解得
,解得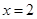 ,
,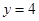 ,所以总人数为
,所以总人数为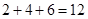 ;
;
(2)由题意得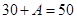 ,
,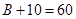 ,
,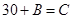 ,
,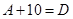 ,
,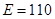 ,
,
解得 ,
,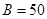 ,
,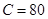 ,
,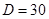 ,
,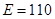 ,
,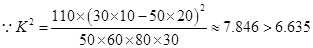 ,
,
因此,大约有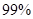 的把握认为海豚身体不健康与受到污染有关;
的把握认为海豚身体不健康与受到污染有关;
(3)设所抽取的两名环保专家记为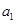 、
、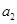 ,
,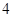 名海洋专家记为
名海洋专家记为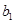 、
、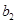 、
、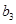 、
、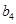 ,
,
则所有的基本事件有: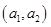 、
、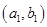 、
、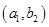 、
、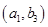 、
、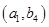 、
、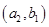 、
、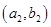 、
、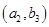 、
、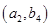 、
、 、
、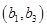 、
、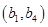 、
、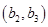 、
、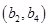 、
、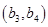 ,
,
记事件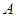 :从研究小组的环保专家和海洋生物专家中随机选
:从研究小组的环保专家和海洋生物专家中随机选 人撰写研究报告求其中恰好有
人撰写研究报告求其中恰好有 人为环保专家,
人为环保专家,
则事件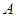 所包含的基本事件有:
所包含的基本事件有: 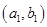 、
、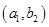 、
、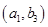 、
、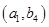 、
、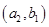 、
、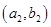 、
、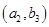 、
、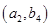 ,共
,共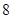 个,
个,
因此,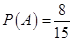 .
.
考点:1.分层抽样;2.独立性检验;3.古典概型

对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
为了了解高一年级学生的身高情况,某校按10%的比例对全校800名高一年级学生按性别进行抽样检查,得到如下频数分布表:
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:男生身高频数分布表
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 频数 | 2 | 12 | 16 | 6 | 3 | 1 |
(1)分别估计高一年级男生和女生的平均身高;
(2)在样本中,从身高180cm以上的男生中任选2人,求至少有一人身高在185cm以上的概率.
某城市随机抽取一个月( 天)的空气质量指数
天)的空气质量指数 监测数据,统计结果如下:
监测数据,统计结果如下:
 |  |  |  |  |  |  |  |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 |  |  |  |  |  |  |  |
(1)根据以上数据估计该城市这
 天空气质量指数
天空气质量指数 的平均值;
的平均值;(2)若该城市某企业因空气污染每天造成的经济损失
 (单位:元)与空气质量指数
(单位:元)与空气质量指数 (记为
(记为 )的
)的关系式为

若在本月
 天中随机抽取一天,试估计该天经济损失
天中随机抽取一天,试估计该天经济损失 大于
大于 元且不超过
元且不超过 元的概率.
元的概率. 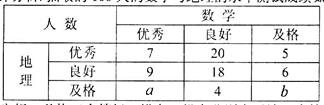
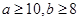 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率. 表示转速(单位转/秒),用
表示转速(单位转/秒),用 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11). )
)