变量与变量有如下对应关系

	2	3	4	5	6
	2.2	3.8	5.5	6.5	7.0

在独立性检验中，统计量有两个临界值：3.841和6.635；当＞3.841时，有95%的把握说明两个事件有关，当＞6.635时，有99%的把握说明两个事件有关，当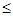3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的=20.87，根据这一数据分析，认为打鼾与患心脏病之间

从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲乙两组数据的平均数分别为，，中位数分别为，，则（    ）

A．，

B．，

C．，

D．，

下图a是某市参加2012年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A₁、A₂、…、A_m [如A₂表示身高（单位：cm）在[150，155]内的学生人数]。图b是统计图a中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160～180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是 （    ）

A．<9

B．<8

C．<7

D．<6

某产品前年的总产量与之间的关系如图所示，已知前年的平均产量最高，则等于

随机抽取某中学甲、乙两面个班10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图甲所示，在这20人中，记身高在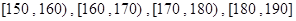内的人数依次为，图乙是统计样本中身高在一定范围内的人数的算法流程图，则下列说法正确的是（  ）
 

若样本+2，+2， ，+2的平均数为10，方差为3，则样本2+3，2+3，… ，2+3，
的平均数、方差、标准差是（   ）

A．19，12，

B．23，12，

C．23，18，

D．19，18，

某产品的广告费用x与销售额y的统计数据如下表

变量x，y有观测数据(x_i，y_i)(i＝1,2，，10)，得散点图(1)；对变量u，v有观测数据( u_i，
v_i)(i ＝1,2，，10)，得散点图(2)．由这两个散点图可以判断．
 

在对某样本进行实验时，测得如下数据：则与之间的回归直线方程为（　　）

	2	1	4	3
	3	2	5	4