题目内容
某产品的广告费用x与销售额y的统计数据如下表
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
 中的
中的 为
为 ,据此模型预报广告费用为7万元时销售额( )
,据此模型预报广告费用为7万元时销售额( )A.63.6万元 B.65.5万元 C.77.9万元 D.74.9万元
D
解析试题分析:由题意,

因为方程 中
中 为
为 ,所以
,所以 ,所以
,所以 ,所以
,所以
所以当 时,
时, .
.
考点:线性回归方程.
点评:本题考查回归方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
某公司有员工49人,其中30岁以上的员工有14人,没超过30岁的员工有35人,为了解员工的健康情况,用分层抽样的方法抽一个容量为7的样本,其中30岁以上的员工应抽多少( )
| A.2人 | B.4人 | C.5人 | D.1人 |
已知二次函数 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 11 | | 1 | -1 | -1 | 1 | 5 |
 的两根分别为
的两根分别为 、
、 ,下面说法错误的是( ) .
,下面说法错误的是( ) .A.
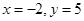 B.
B.
C.当
 时,
时,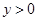 D.当
D.当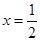 时,
时, 有最小值
有最小值 设有一个直线回归方程为y=2-1.5x,则变量x增加一个单位时 ( )
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
对变量 有观测数据(
有观测数据( ,
, )(
)( ),得散点图1;对变量
),得散点图1;对变量 有观测数据(
有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
将参加夏令营的600名学生编号为:001,002,…,600. 采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )
| A.26, 16, 8, | B.25,17,8 | C.25,16,9 | D.24,17,9 |
为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( )
| A.20 | B.30 | C.40 | D.50 |
有A,B,C三种零件,分别为a个,300个,b个.采用分层抽样法抽取一个容量为45的样本,A种零件被抽取20个,C种零件被抽取10个,这三种零件共( )个
| A.900 | B.850 | C.800 | D.750 |
 ,
, ,中位数分别为
,中位数分别为 ,
, ,则( )
,则( )
 ,
,

 ,
,