极坐标系中,由三条曲线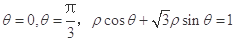 围成的图形的面积是( )
围成的图形的面积是( )
A.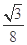 | B.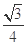 | C.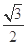 | D. |
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=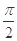 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=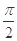 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.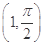 | B.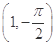 | C.(1,0) | D.(1,π) |
极坐标方程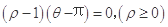 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.一个圆和一条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
已知椭圆 、抛物线
、抛物线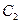 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和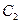 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 | 3 |  2 2 | 4 |  |
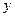 |  | 0 |  4 4 |  |
 的标准方程;
的标准方程;(Ⅱ)请问是否存在直线
 满足条件:①过
满足条件:①过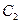 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足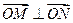 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. 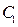 的方程为
的方程为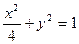 ,双曲线
,双曲线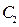 的左、右焦
的左、右焦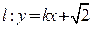 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。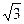 )的直线l过点(0,-2
)的直线l过点(0,-2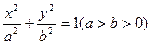
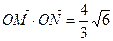 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存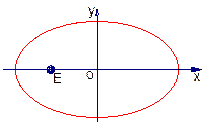
 的离心率
的离心率 ,且椭圆过点
,且椭圆过点 .
. 的方程;
的方程; 为椭圆
为椭圆 为椭圆的右焦点,以
为椭圆的右焦点,以 长为半径作圆
长为半径作圆 作圆
作圆 ,(
,( 为切点),求点
为切点),求点 的面积最大.]
的面积最大.]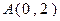 ,右焦点
,右焦点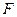 与点
与点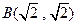 的距离为
的距离为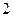 .
.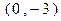 的直线
的直线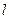 ,使直线
,使直线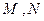 满足
满足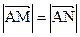 ?若存在,求出直线
?若存在,求出直线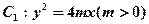 的准线与x轴交于点
的准线与x轴交于点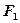 ,
,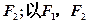 为焦点,离心率为
为焦点,离心率为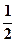 的椭圆
的椭圆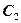 与抛物线
与抛物线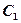 在x轴上方的交点为P
在x轴上方的交点为P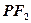 交抛物线于点Q,M是抛物线
交抛物线于点Q,M是抛物线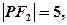 且P点横坐标为
且P点横坐标为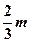 ,求面积
,求面积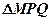 的最大值
的最大值