圆 的圆心坐标是( )
的圆心坐标是( )
| A.(2,3) | B.(-2,3) | C.(-2,-3) | D.(2,-3) |
将圆 平分的直线的方程可以是 ( )
平分的直线的方程可以是 ( )
A. | B. | C.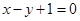 | D. |
设椭圆 的离心率为
的离心率为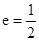 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点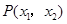 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
已知 为坐标原点,直线
为坐标原点,直线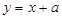 与圆
与圆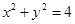 分别交于
分别交于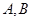 两点.若
两点.若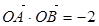 ,则实数
,则实数 的值为( )
的值为( )
| A.1 | B.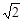 | C.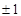 | D.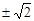 |
已知直线 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 后所得直线与圆
后所得直线与圆 相切,,则
相切,,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
已知实数 满足
满足 ,则
,则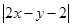 的最小值是( )
的最小值是( )
A. | B. | C. | D.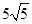 |
直线 被圆
被圆 截得的弦长为 ( )
截得的弦长为 ( )
A. | B. | C. | D.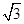 |
已知函数 集合
集合
 ,则
,则 的面积是( )
的面积是( )
A. | B. | C. | D. |
设椭圆 +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
| A.必在圆x2+y2=2内 | B.必在圆x2+y2=2上 |
| C.必在圆x2+y2=2外 | D.以上三种情形都有可能 |
 与圆
与圆 的位置关系为( )
的位置关系为( )