题目内容
直线 被圆
被圆 截得的弦长为 ( )
截得的弦长为 ( )
A. | B. | C. | D.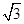 |
D
解析试题分析:将圆的方程化为标准式得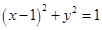 ,圆心坐标为
,圆心坐标为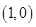 ,半径长为
,半径长为 ,故圆心到直线
,故圆心到直线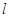 的距离
的距离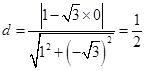 ,故直线
,故直线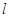 被圆截得的弦长为
被圆截得的弦长为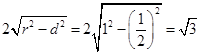 ,选D.
,选D.
考点:1.点到直线的距离;2.勾股定理

练习册系列答案
相关题目
圆 关于直线
关于直线 成轴对称图形,则
成轴对称图形,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
若点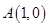 和点
和点 到直线
到直线 的距离依次为
的距离依次为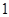 和
和 ,则这样的直线有( )
,则这样的直线有( )
A.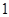 条 条 | B. 条 条 | C. 条 条 | D. 条 条 |
已知点 满足方程
满足方程 ,则由点
,则由点 向圆
向圆 所作的切线长的最小值是( )
所作的切线长的最小值是( )
A. | B. | C. | D. |
圆 的切线方程中有一个是( )
的切线方程中有一个是( )
| A.x-y=0 | B.x+y=0 | C.x=0 | D.y=0 |
设椭圆 的离心率为
的离心率为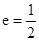 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点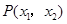 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
垂直于直线 与圆
与圆 相切于第一象限的直线方程是( )
相切于第一象限的直线方程是( )
A. | B. | C. | D. |
圆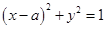 与直线
与直线 相切于第三象限,则
相切于第三象限,则 的值是( ).
的值是( ).
A. | B. | C. | D. |
 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,C是圆心,那么四边形PACB面积的最小值( )
的两条切线,C是圆心,那么四边形PACB面积的最小值( ) B.2
B.2 D.2
D.2