题目内容
已知函数 集合
集合
 ,则
,则 的面积是( )
的面积是( )
A. | B. | C. | D. |
B
解析试题分析:由题意可知,因为 所以集合
所以集合
 ,集合
,集合 中的元素为以点
中的元素为以点 为圆心,以
为圆心,以 为半径的圆以及圆内的点;集合
为半径的圆以及圆内的点;集合
 ,集合
,集合 中的元素为夹在直线
中的元素为夹在直线 和直线
和直线 之间左右两部分平面区域中的点,所以
之间左右两部分平面区域中的点,所以 表示的区域是在圆内且夹在两条直线之间的左右两部分,因为直线
表示的区域是在圆内且夹在两条直线之间的左右两部分,因为直线 和直线
和直线 互相垂直,所以它的面积是半径为
互相垂直,所以它的面积是半径为 的圆的面积一半,
的圆的面积一半, ,故选B.
,故选B.
考点:本题考查了集合的基本运算,圆和直线关系的综合应用,以及线性规划的应用,解题的关键步骤是判断出集合 和
和 的图形,解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.
的图形,解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
直线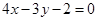 与圆
与圆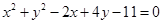 的位置关系是( )
的位置关系是( )
| A.相离 | B.相切 | C.相交过圆心 | D.相交不过圆心 |
若点 和点
和点 到直线
到直线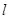 的距离依次为
的距离依次为 和
和 ,则这样的直线有( )
,则这样的直线有( )
A. 条 条 | B. 条 条 | C. 条 条 | D. 条 条 |
在平面直角坐标系内,若圆 :
: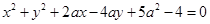 的圆心在第二象限内,则实数
的圆心在第二象限内,则实数 的取值范围为( )
的取值范围为( )
A.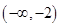 | B.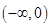 | C.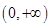 | D.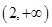 |
已知直线 与曲线
与曲线 有交点,则( )
有交点,则( )
A. | B. | C. | D. |
已知 为坐标原点,直线
为坐标原点,直线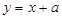 与圆
与圆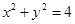 分别交于
分别交于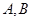 两点.若
两点.若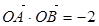 ,则实数
,则实数 的值为( )
的值为( )
| A.1 | B.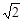 | C.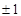 | D.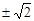 |
已知直线 与直线
与直线
 平行且与圆
平行且与圆 相切,则直线
相切,则直线 的方程为( )
的方程为( )
A. | B. 或 或 |
C. | D. 或 或 |
直线 与圆
与圆
 的位置关系是( )
的位置关系是( )
| A.相切 | B.相交且直线不经过圆心 |
| C.相离 | D.相交且直线经过圆心 |
 :
:
 ,若以点
,若以点 为圆心的圆与直线
为圆心的圆与直线 ,且
,且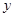 轴上,则该圆的方程为( )
轴上,则该圆的方程为( )


