设m,n是两条不同的直线,α,β是两个不同的平面( ).
| A.若m∥α,n∥α,则m∥n |
| B.若m∥α,m∥β,则α∥β |
| C.若m∥n,m⊥α,则n⊥α |
| D.若m∥α,α⊥β,则m⊥β |
设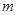 ,
, 是两条不同的直线,
是两条不同的直线,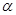 ,
,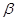 ,
,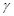 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题:
①若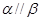 ,
,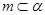 ,
,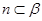 ,则
,则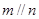 ;
;
②若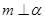 ,
,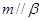 ,则
,则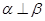 ;
;
③ 若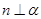 ,
,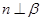 ,
,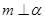 ,则
,则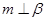 ;
;
④ 若 ,
,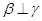 ,
,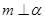 ,则
,则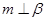 .
.
其中错误命题的序号是( )
| A.①④ | B.①③ | C.②③④ | D.②③ |
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )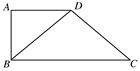
| A.平面ABD⊥平面ABC | B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC | D.平面ADC⊥平面ABC |
在棱长为1的正方体 中,
中, 分别为线段
分别为线段 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.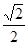 |
设一地球仪的球心为空间直角坐标系的原点 ,球面上有两个点
,球面上有两个点 的坐标分别为
的坐标分别为 ,则
,则 ( )
( )
| A.18 | B.12 | C. | D. |
设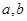 是两条不同的直线,
是两条不同的直线,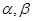 是两个不同的平面,则能得出
是两个不同的平面,则能得出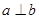 的是( )
的是( )
A.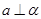 , , , ,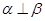 | B.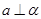 , ,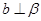 , , |
C. , ,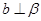 , , | D. , , , ,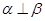 |
下面四个命题:
①“直线a∥直线b”的充分条件是“直线a平行于直线b所在的平面”;
②“直线l⊥平面α”的充要条件是“直线垂直平面α内无数条直线”;
③“直线a,b不相交”的必要不充分条件是“直线a,b为异面直线”;
④“平面α∥平面β”的必要不充分条件是“平面α内存在不共线三点到平面β的距离相等”.
其中为真命题的序号是( )
| A.①② | B.②③ | C.③④ | D.④ |
设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列为真命题的是( )
| A.若α⊥β,m⊥α,则m∥β | B.若α⊥γ,β⊥γ,则α∥β |
| C.若m⊥α,n∥m,则n⊥α | D.若m∥α,n∥α,则m∥n |
 ,直线
,直线 ,且有
,且有 ,则下列四个命题正确的个数为( )
,则下列四个命题正确的个数为( ) ∥
∥ 则
则 ;②若
;②若 ∥
∥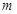 则
则 则
则 ;
;



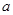 ∥
∥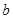 ,
,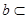 平面
平面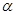 ,则
,则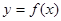 定义域内存在
定义域内存在 满足
满足
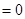 ,则
,则