[2013·安徽高考]在下列命题中,不是公理的是( )
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
类比平面内 “垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:
①垂直于同一条直线的两条直线互相平行 ②垂直于同一个平面的两条直线互相平行
③垂直于同一条直线的两个平面互相平行 ④垂直于同一个平面的两个平面互相平行,则正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
已知是两条不同直线,是两个不同的平面,给出下列命题:
①若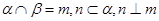 ,则
,则 ;②若
;②若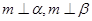 ,则
,则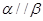 ;③若
;③若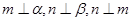 ,则
,则 ;④若
;④若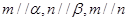 ,则
,则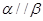 ,其中正确的命题是( )
,其中正确的命题是( )
| A.①② | B.②③ | C.③④ | D.①③ |
已知平面 、
、 和直线
和直线 ,给出条件:①
,给出条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
由这五个条件中的两个同时成立能推导出 的是( )
的是( )
| A.①④ | B.①⑤ | C.②⑤ | D.③⑤ |
设m,n是两条不同的直线,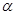 、
、 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥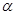 ,n ,n  ,m⊥n ,m⊥n 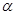 ⊥ ⊥ |
B.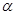 ⊥ ⊥ , ,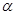 ∩ ∩ =m,n⊥m =m,n⊥m n⊥ n⊥ |
C.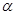 ⊥ ⊥ ,m⊥ ,m⊥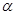 ,n∥ ,n∥  m⊥n m⊥n |
D.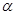 ∥ ∥ ,m⊥ ,m⊥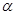 ,n∥ ,n∥  m⊥n m⊥n |
设m,n是两条不同的直线, ,
, 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥ ,n ,n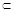  ,m⊥n ,m⊥n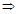  ⊥ ⊥ | B. ⊥ ⊥ , , ∩ ∩ =m,n⊥m =m,n⊥m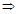 n⊥ n⊥ |
C. ⊥ ⊥ ,m⊥ ,m⊥ ,n∥ ,n∥ 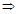 m⊥n m⊥n | D. ∥ ∥ ,m⊥ ,m⊥ ,n∥ ,n∥ 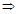 m⊥n m⊥n |
已知直线 ,
, 与平面
与平面 ,
, ,
, ,满足
,满足 ,
, ,
, ,
, ,则必有( )
,则必有( )
A. 且 且 | B. 且 且 | C. 且 且 | D. 且 且 |
已知正四棱柱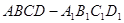 中,
中, ,
,  为
为 的中点,则点
的中点,则点 到平面
到平面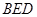 的距离为()
的距离为()
| A.1 | B.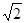 | C. | D.2 |
 ,
, ,M、N分别是BC、AB的中点,沿直线MN将折起,使二面角
,M、N分别是BC、AB的中点,沿直线MN将折起,使二面角 的大小为
的大小为 ,则
,则 与平面ABC所成角的正切值为( )
与平面ABC所成角的正切值为( ) B.
B. C.
C. D.
D.

 、
、 是两条直线,
是两条直线, 、
、 是两个平面,给出下列命题:①若
是两个平面,给出下列命题:①若 ,
, ,则
,则 ;②若平面
;②若平面 ,
, ,
, ,
, ,则
,则 个
个 个
个 个
个 个
个