题目内容
设m,n是两条不同的直线, ,
, 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥ ,n ,n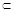  ,m⊥n ,m⊥n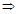  ⊥ ⊥ | B. ⊥ ⊥ , , ∩ ∩ =m,n⊥m =m,n⊥m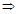 n⊥ n⊥ |
C. ⊥ ⊥ ,m⊥ ,m⊥ ,n∥ ,n∥ 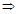 m⊥n m⊥n | D. ∥ ∥ ,m⊥ ,m⊥ ,n∥ ,n∥ 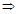 m⊥n m⊥n |
D
解析试题分析:试题分析:A选项中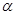 、
、 可能平行也可能相交,所以A不正确;B选项中
可能平行也可能相交,所以A不正确;B选项中 和
和 可能平行、可能相交还可能线在面内,所以B不正确;C选项中
可能平行、可能相交还可能线在面内,所以B不正确;C选项中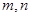 两直线可能相交、平行或异面,所以C不正确;D选项中
两直线可能相交、平行或异面,所以C不正确;D选项中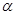 ∥
∥ ,m⊥
,m⊥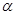
 ,因为n∥
,因为n∥ ,所以
,所以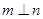 ,故D正确.
,故D正确.
考点:线线、线面、面面的位置关系.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
如图所示,正三棱锥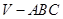 中,
中, 分别是
分别是 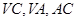 的中点,
的中点,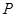 为
为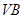 上任意一点,则直线
上任意一点,则直线 与
与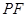 所成的角的大小是 ( )
所成的角的大小是 ( )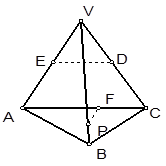
A.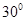 | B.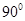 | C.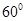 | D.随 点的变化而变化. 点的变化而变化. |
从正方体六个面的对角线中任取两条作为一对,其中所成的角为 的共有( )
的共有( )
| A.24对 | B.30对 | C.48对 | D.60对 |
已知是两条不同直线,是两个不同的平面,给出下列命题:
①若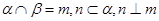 ,则
,则 ;②若
;②若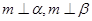 ,则
,则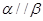 ;③若
;③若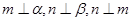 ,则
,则 ;④若
;④若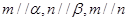 ,则
,则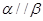 ,其中正确的命题是( )
,其中正确的命题是( )
| A.①② | B.②③ | C.③④ | D.①③ |
已知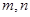 是两条不同直线,
是两条不同直线,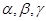 是三个不同平面,则下列正确的是 ( )
是三个不同平面,则下列正确的是 ( )
A.若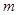 ∥ ∥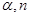 ∥ ∥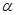 ,则 ,则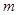 ∥ ∥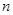 | B.若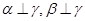 ,则 ,则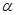 ∥ ∥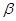 |
C.若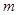 ∥ ∥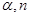 ∥ ∥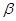 ,则 ,则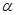 ∥ ∥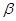 | D.若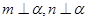 ,则 ,则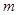 ∥ ∥ |
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )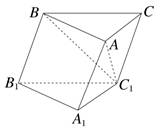
| A.直线AB上 | B.直线BC上 |
| C.直线AC上 | D.△ABC内部 |
如图是正方体的展开图,则在这个正方体中: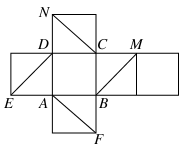
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A.①②③ | B.②④ | C.③④ | D.②③④ |
[2012·安徽高考]设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |