观察下列数的特点,1,1,2,3,5,8,x,21,34,55,…中,其中x是( )
| A.12 | B.13 | C.14 | D.15 |
已知数列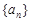 的通项公式
的通项公式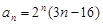 ,则数列
,则数列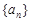 的前
的前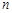 项和
项和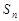 取得最小值时
取得最小值时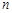 的值为( )
的值为( )
A.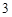 | B.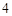 | C.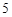 | D.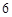 |
已知数列{an}满足an = nkn(n∈N*,0 < k < 1),下面说法正确的是( )
①当 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当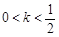 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当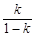 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
| A.①② | B.②④ | C.③④ | D.②③ |
在数列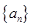 中,
中, ,
,  ,则
,则 =( )
=( )
A. | B. | C. | D. |
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
已知数列{an}满足a1=1,an+1= ,则其前6项之和是( )
,则其前6项之和是( )
| A.16 | B.20 | C.33 | D.120 |
设 ,当
,当 时,
时,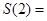 ( )
( )
A.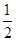 | B.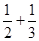 | C.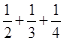 | D.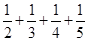 |
已知数列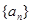 的前
的前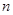 项和为
项和为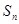 ,且
,且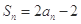 则
则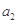 等于( )
等于( )
| A.4 | B.2 | C.1 | D.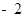 |
已知数列2,5,11,20,x,47, 合情推出x的值为( )
| A.29 | B.31 | C.32 | D.33 |
[2013·江西抚州月考]数列{an}的前n项积为n2,那么当n≥2时,{an}的通项公式为( )
| A.an=2n-1 | B.an=n2 |
C.an= | D.an= |