已知 是
是 所在平面内的一点,且满足
所在平面内的一点,且满足 ,则点
,则点 是
是 的 ( )
的 ( )
| A.内心 | B.外心 | C.垂心 | D.重心 |
如图,在△ 中,
中, ,
, 是
是 上的一点,若
上的一点,若 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C.1 | D.3 |
平面向量的集合 到
到 的映射
的映射 由
由 确定,其中
确定,其中 为常向量.若映射
为常向量.若映射 满足
满足 对
对 恒成立,则
恒成立,则 的坐标不可能是 ( )
的坐标不可能是 ( )
A. | B. |
C. | D. |
法向量为 的直线,其斜率为( )
的直线,其斜率为( )
A. | B. | C. | D. |
若等边 的边长为2,平面内一点M满足
的边长为2,平面内一点M满足 ,则
,则
A. | B. | C. | D. |
平行六面体 中,设
中,设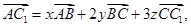 则
则 ( )
( )
| A.1 | B. | C. | D.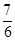 |
在 中,
中, 为边
为边 中线
中线 上的一点,若
上的一点,若 ,则
,则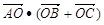 的( )
的( )
| A.最大值为8 | B.最大值为4 | C.最小值-4 | D.最小值为-8 |
已知非零向量 与
与 满足(
满足( +
+ )·
)· =0,且
=0,且 ·
· =-
=-
,则△ABC为( )
| A.等腰非等边三角形 | B.等边三角形 |
| C.三边均不相等的三角形 | D.直角三角形 |
 ,下列条件中能确定的M与点A、B、C一定共面的是( )
,下列条件中能确定的M与点A、B、C一定共面的是( )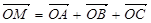
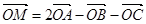
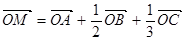
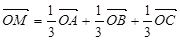
 则
则 的值为( )
的值为( )


