题目内容
已知非零向量 与
与 满足(
满足( +
+ )·
)· =0,且
=0,且 ·
· =-
=-
,则△ABC为( )
| A.等腰非等边三角形 | B.等边三角形 |
| C.三边均不相等的三角形 | D.直角三角形 |
A
解析试题分析:注意到 表示与
表示与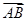 同向的单位向量,
同向的单位向量, 表示与
表示与 同向的单位向量,所以
同向的单位向量,所以 +
+ 表示以与
表示以与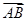 同向的单位向量和与
同向的单位向量和与 同向的单位向量为邻边的平行四边形的对角线,因为(
同向的单位向量为邻边的平行四边形的对角线,因为( +
+ )·
)· =0,所以
=0,所以 ;由
;由 ·
· =-
=- 可以得出
可以得出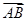 与
与 夹角为
夹角为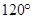 ,所以△ABC为等腰非等边三角形.
,所以△ABC为等腰非等边三角形.
考点:本小题主要考查向量加法的平行四边形法则、向量垂直的应用和向量数量积的应用,考查了学生综合分析问题解决问题的能力.
点评:注意到 表示与
表示与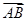 同向的单位向量是解决此题的关键,而向量加法的平行四边形法则的应用也是解题时经常用到的内容.
同向的单位向量是解决此题的关键,而向量加法的平行四边形法则的应用也是解题时经常用到的内容.

练习册系列答案
相关题目
已知O是锐角△ABC的外接圆圆心,∠A=60°, ,则m的值为( )
,则m的值为( )
A. | B. | C.1 | D. |
△ 外接圆的半径为
外接圆的半径为 ,圆心为
,圆心为 ,且
,且 ,
,  ,则
,则 等于
等于
A. | B. | C. | D.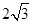 |
已知两个非零向量 与
与 ,定义
,定义 ,其中
,其中 为
为 与
与 的夹角.若
的夹角.若 ,
,  ,则
,则 的值为
的值为
A. | B. | C. | D. |
与向量 =(
=( ,1),
,1), =(1,
=(1, )的夹角相等且模为
)的夹角相等且模为 的向量为 ( )
的向量为 ( )
A. | B. |
C. | D. |
法向量为 的直线,其斜率为( )
的直线,其斜率为( )
A. | B. | C. | D. |
在△ 中,
中, 是
是 的中点,
的中点, ,点
,点 在
在 上,且满足
上,且满足 ,则
,则
A. | B. | C. | D. |
 ,
, ,且
,且 ,
, ,则向量
,则向量 =_________.
=_________. ,若
,若 ,则
,则 .
.