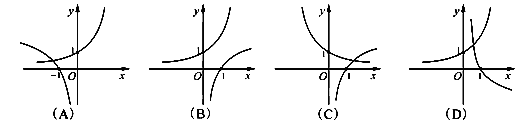
对于定义域是R的任意奇函数 有( ).
有( ).
A.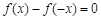 | B. | C.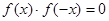 | D.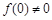 |
已知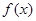 是R上最小正周期为2的周期函数,且当
是R上最小正周期为2的周期函数,且当 时,
时, ,则函数
,则函数 在区间
在区间 上的图像与x轴的交点个数为( )
上的图像与x轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
已知函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, 则函数
则函数 =
= 在
在 上的所有零点之和为
上的所有零点之和为
| A.7 | B.8 | C.9 | D.10 |
已知函数 ,且关于x的方程
,且关于x的方程 有6个不同的实数解,若最小实数解为
有6个不同的实数解,若最小实数解为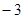 ,则
,则 的值为( )
的值为( )
| A.-3 | B.-2 | C.0 | D.不能确定 |
下列各组函数是同一函数的是( )
①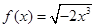 与
与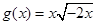 ; ②
; ②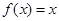 与
与 ;
;
③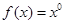 与
与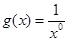 ; ④
; ④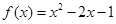 与
与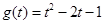 。
。
| A.①② | B.①③ | C.③④ | D.①④ |
已知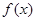 在
在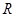 上是减函数,则满足
上是减函数,则满足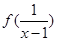 >
> 的实数
的实数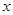 的取值范围是( ).
的取值范围是( ).
| A.(-∞,1) | B.(2,+∞) |
| C.(-∞,1)∪(2,+∞) | D.(1,2) |
将函数 的图像先向左平移2个单位,在向下平移3 个单位后对应的解析式是( )
的图像先向左平移2个单位,在向下平移3 个单位后对应的解析式是( )
A.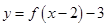 | B. |
C. | D. |
设 ,用二分法求方程
,用二分法求方程 内近似解的过程中得
内近似解的过程中得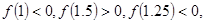 则方程的根落在区间( )
则方程的根落在区间( )
A. | B. | C. | D.不能确定 |
定义方程 的实数根
的实数根 叫做函数
叫做函数 的“新驻点”,若函数
的“新驻点”,若函数
 的“新驻点”分别为
的“新驻点”分别为 ,则
,则 的大小关系为
的大小关系为
A. | B. | C. | D. |
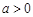 ,
,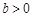 ,且
,且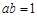 ,则函数
,则函数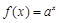 与函数
与函数 的图象可能是
的图象可能是