函数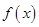 的部分图象如图所示,则
的部分图象如图所示,则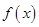 的解析式可以是
的解析式可以是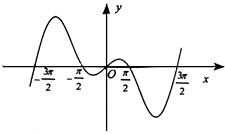
A.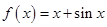 | B.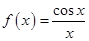 |
C.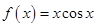 | D. |
下列函数是偶函数,且在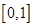 上单调递增的是
上单调递增的是
A. | B.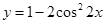 |
C.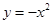 | D.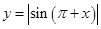 |
设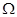 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从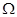 中的任意一点
中的任意一点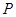 作
作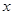 轴、
轴、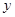 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
,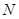 ,记点
,记点 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为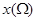 ,点
,点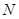 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为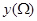 .如果
.如果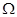 是边长为1的正方形,那么
是边长为1的正方形,那么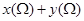 的取值范围是( )
的取值范围是( )
A.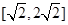 | B.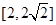 | C.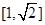 | D.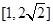 |
设函数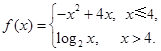 若函数
若函数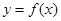 在区间
在区间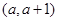 上单调递增,则实数
上单调递增,则实数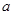 的取值范围是( )
的取值范围是( )
A.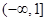 | B.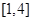 |
C.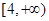 | D.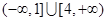 |
设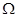 为平面直角坐标系
为平面直角坐标系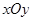 中的点集,从
中的点集,从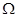 中的任意一点
中的任意一点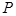 作
作 轴、
轴、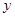 轴的垂线,垂足分别为
轴的垂线,垂足分别为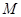 ,
, ,记点
,记点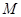 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为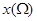 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为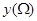 . 若
. 若 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
①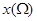 的最大值为
的最大值为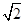 ;
;
②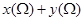 的取值范围是
的取值范围是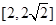 ;
;
③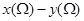 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①② | D.①②③ |
(2013•重庆)函数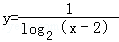 的定义域为( )
的定义域为( )
| A.(﹣∞,2) | B.(2,+∞) |
| C.(2,3)∪(3,+∞) | D.(2,4)∪(4,+∞) |
(2013•重庆)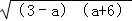 (﹣6≤a≤3)的最大值为( )
(﹣6≤a≤3)的最大值为( )
| A.9 | B.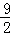 | C.3 | D.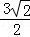 |
下图揭示了一个由区间 到实数集
到实数集 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线 与
与 轴交于点
轴交于点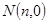 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( )
 ;
;  是偶函数;
是偶函数;  在其定义域上是增函数;
在其定义域上是增函数;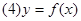 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4). | B.(1)(2)(3). | C.(1)(2)(4). | D.(1)(2)(3)(4). |
下列函数中,与函数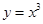 的值域相同的函数为 ( )
的值域相同的函数为 ( )
A.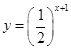 . . | B.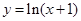 . . | C.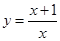 . . | D.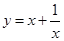 . . |
下图揭示了一个由区间 到实数集
到实数集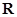 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线 与
与 轴交于点
轴交于点 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( ) ;
; 是偶函数;
是偶函数; 在其定义域上是增函数;
在其定义域上是增函数; 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4) | B.(1)(2)(3) |
| C.(1)(2)(4) | D.(1)(2)(3)(4). |