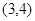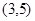观察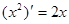 ,
,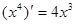 ,
,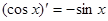 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数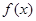 满足
满足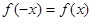 ,记
,记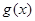 为
为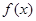 的导函数,则
的导函数,则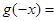 ( )
( )
A.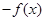 | B.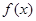 | C.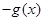 | D.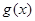 |
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )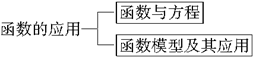
| A.“函数与方程”的上位 | B.“函数与方程”的下位 |
| C.“函数模型及其应用”的上位 | D.“函数模型及其应用”的下位 |
已知函数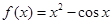 ,则
,则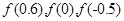 的大小关系是( )
的大小关系是( )
A.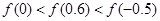 |
B.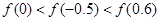 |
C.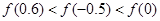 |
D.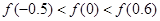 |
下列函数中,既是偶函数又在区间 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
已知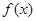 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则函数
,则函数 的零点的集合为( )
的零点的集合为( )
A. | B. | C. | D. |
已知函数 ,在下列区间中,包含
,在下列区间中,包含 零点的区间是( )
零点的区间是( )
A. | B. | C. | D. |
 ,另一种平均价格曲线
,另一种平均价格曲线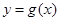 ,如
,如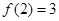 表示股票开始买卖后2小时的即时价格为3元;
表示股票开始买卖后2小时的即时价格为3元; 表示2小时内的平均价格为3元.下面给出了四个图像,实线表示
表示2小时内的平均价格为3元.下面给出了四个图像,实线表示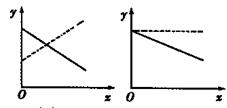
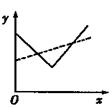
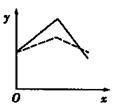
 的大致图像是( )
的大致图像是( )
 定义域为
定义域为 ,且函数
,且函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,
时, ,(其中
,(其中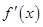 是
是 的导函数),若
的导函数),若 ,
, ,则
,则 的大小关系是( )
的大小关系是( )
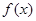 为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间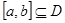 (其中
(其中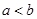 ),使得当
),使得当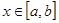 时,
时,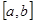 ,则称函数
,则称函数 是
是 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )