题目内容
已知数列 .
.
(I)求证数列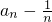 成等比数列,并求数列{an}的通项公式;
成等比数列,并求数列{an}的通项公式;
(II)若bn=nan,求数列{bn}的前n项和Sn;
(III)求证: .
.
证明:(I)∵ ,∴数列
,∴数列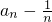 是以1为首项,2为公比的等比数列,∴
是以1为首项,2为公比的等比数列,∴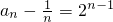 ,∴
,∴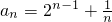
(II)∵bn=nan=n•2n-1+1,∴Sn=b1+b2++bn=(1+2×21++n×2n-1)+n
记∴Tn=1+2×21++n×2n-1,于是2Tn=2+2×22++n×2n,两式相减化简得Tn=(n-1)×2n+1,∴数列{bn}的前n项和Sn=(n-1)×2n+n+1;
(III)由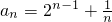 知
知
当n≥2时, 知
知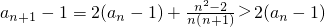 ,∴
,∴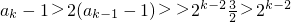 即
即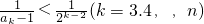
当n=1,2时,结论成立.
当n≥3时,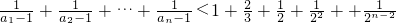 =
= ,∴
,∴
分析:(I)由 ,可得
,可得 ,所以可证数列
,所以可证数列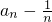 是以1为首项,2为公比的等比数列,进而可求数列{an}的通项公式;
是以1为首项,2为公比的等比数列,进而可求数列{an}的通项公式;
(II)因为bn=nan=n•2n-1+1,所以Sn=b1+b2++bn=(1+2×21++n×2n-1)+n
记Tn=1+2×21++n×2n-1,于是2Tn=2+2×22++n×2n,错位相减得Tn=(n-1)×2n+1,从而可求数列{bn}的前n项和Sn;
(III)由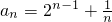 知
知 ,当n≥2时,
,当n≥2时, 知
知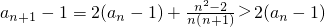 ,从而有
,从而有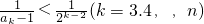 进而可用放缩法转化为等比数列求和,故问题得证.
进而可用放缩法转化为等比数列求和,故问题得证.
点评:本题考查等比、等差数列、不等式和数列的有关知识,化归、递推等数学思想方法,同时考查运算能力,推理论证以及综合运用有关知识分析解决问题的能力.
 ,∴数列
,∴数列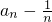 是以1为首项,2为公比的等比数列,∴
是以1为首项,2为公比的等比数列,∴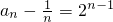 ,∴
,∴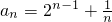
(II)∵bn=nan=n•2n-1+1,∴Sn=b1+b2++bn=(1+2×21++n×2n-1)+n
记∴Tn=1+2×21++n×2n-1,于是2Tn=2+2×22++n×2n,两式相减化简得Tn=(n-1)×2n+1,∴数列{bn}的前n项和Sn=(n-1)×2n+n+1;
(III)由
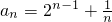 知
知
当n≥2时,
 知
知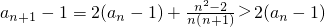 ,∴
,∴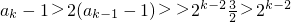 即
即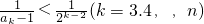
当n=1,2时,结论成立.
当n≥3时,
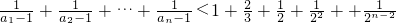 =
= ,∴
,∴
分析:(I)由
 ,可得
,可得 ,所以可证数列
,所以可证数列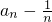 是以1为首项,2为公比的等比数列,进而可求数列{an}的通项公式;
是以1为首项,2为公比的等比数列,进而可求数列{an}的通项公式;(II)因为bn=nan=n•2n-1+1,所以Sn=b1+b2++bn=(1+2×21++n×2n-1)+n
记Tn=1+2×21++n×2n-1,于是2Tn=2+2×22++n×2n,错位相减得Tn=(n-1)×2n+1,从而可求数列{bn}的前n项和Sn;
(III)由
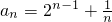 知
知 ,当n≥2时,
,当n≥2时, 知
知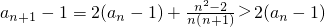 ,从而有
,从而有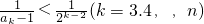 进而可用放缩法转化为等比数列求和,故问题得证.
进而可用放缩法转化为等比数列求和,故问题得证.点评:本题考查等比、等差数列、不等式和数列的有关知识,化归、递推等数学思想方法,同时考查运算能力,推理论证以及综合运用有关知识分析解决问题的能力.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
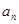 }中
}中
 ,求证数列{
,求证数列{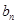 }是等比数列;
}是等比数列;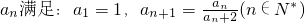 .
.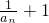 是等比数列;
是等比数列;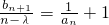 ,且数列{bn}是单调递增数列,求实数λ的取值范围.
,且数列{bn}是单调递增数列,求实数λ的取值范围.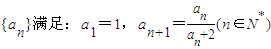 .
.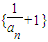 是等比数列;
是等比数列;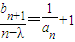 ,且数列{bn}是单调递增数列,求实数λ的取值范围.
,且数列{bn}是单调递增数列,求实数λ的取值范围. .
. 成等比数列,并求数列{an}的通项公式;
成等比数列,并求数列{an}的通项公式; .
.