题目内容
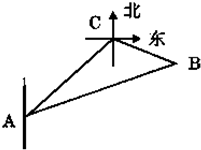 一缉私艇在A处发现在北偏东45°方向距离12海里的海面上C处有一走私船正以10海里/小时的速度沿东偏南15°方向逃窜,缉私艇的速度为14海里/小时.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需时间和α角的正弦值.
一缉私艇在A处发现在北偏东45°方向距离12海里的海面上C处有一走私船正以10海里/小时的速度沿东偏南15°方向逃窜,缉私艇的速度为14海里/小时.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需时间和α角的正弦值.分析:利用余弦定理在△ABC中求出x,然后利用正弦定理
=
求出α角的正弦值.
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
解答:解:设A,C分别表示缉私艇,走私船的位置,设经过x时后在B处追上,
则有 AB=14x,BC=10x,∠ACB=120°,…..(2分)
由余弦定理得AB2=AC2+BC2-2•AC•BCcos∠ACB…(4分)
∴(14x)2=122+(10x)2-2×12×10x×cos120°…..(6分)
∴x=2…..(8分)
∴AB=28,BC=20,
正弦定理得
=
…..(10分)
∴sinα=sin∠BAC=
=
所以所需时间2小时,sinα=
…(12分)
则有 AB=14x,BC=10x,∠ACB=120°,…..(2分)
由余弦定理得AB2=AC2+BC2-2•AC•BCcos∠ACB…(4分)
∴(14x)2=122+(10x)2-2×12×10x×cos120°…..(6分)
∴x=2…..(8分)
∴AB=28,BC=20,
正弦定理得
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
∴sinα=sin∠BAC=
| 20sin120° |
| 28 |
5
| ||
| 14 |
所以所需时间2小时,sinα=
5
| ||
| 14 |
点评:本题考查正弦定理以及余弦定理的应用,考查计算能力.

练习册系列答案
相关题目
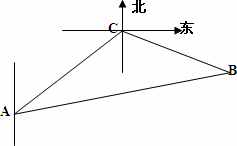
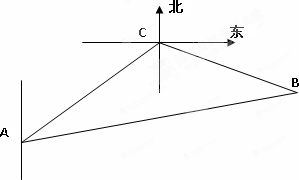
 方向,距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东 的方向去追,求追及所需的时间和
的方向去追,求追及所需的时间和 角的正弦值.
角的正弦值.