题目内容
若三棱锥S ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2
ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2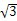 ,AB=1,AC=2,∠BAC=60°,则球O的表面积为 .
,AB=1,AC=2,∠BAC=60°,则球O的表面积为 .
16π解析:因为AB=1,AC=2,∠BAC=60°,
所以BC2=1+22-2×1×2cos 60°=3,
所以BC=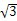 .
.
所以∠ABC=90°,
即△ABC为直角三角形.
因为三棱锥S ABC的所有顶点都在球O的球面上,
ABC的所有顶点都在球O的球面上,
且SA⊥平面ABC,
于是SC为球O的直径.
Rt△SAC中,SA=2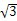 ,AC=2,
,AC=2,
所以SC=4.
球的表面积为4π( )2=16π.
)2=16π.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.

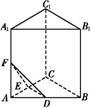
 A1B1C1中,AB=AA1,则AC1与平面BB1C1C所成角的正弦值为( )
A1B1C1中,AB=AA1,则AC1与平面BB1C1C所成角的正弦值为( ) (B)
(B) (C)
(C) (D)
(D)