题目内容
已知函数f(x)=ax3+bx2-x(x∈R,a、b是常数,a≠0),且当x=1和x=2时,函数f(x)取得极值.(I)求函数f(x)的解析式;
(Ⅱ)若曲线y=f(x)与g(x)=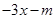
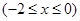 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围.
(Ⅱ)若曲线y=f(x)与g(x)=
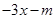
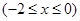 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围. (I)  (Ⅱ) 0≤m<
(Ⅱ) 0≤m<
 (Ⅱ) 0≤m<
(Ⅱ) 0≤m<
试题分析:解:(1)
 ,依题意,
,依题意, ,即
,即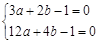 ,
,解得
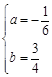 ,经检验
,经检验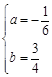 符合题意。∴
符合题意。∴
(2) 曲线y=f(x)与g(x)两个不同的交点,
即
 在[-2,0]有两个不同的实数解
在[-2,0]有两个不同的实数解 设φ(x)=
 ,则
,则 ,
, 由
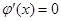 ,得x= 4或x= -1,∵x∈[-2,0],
,得x= 4或x= -1,∵x∈[-2,0],∴当x(-2,-1)时,
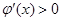 ,于是φ(x)在[-2,-1]上递增;
,于是φ(x)在[-2,-1]上递增;当x(-1,0)时,
 ,于是φ(x)在[-1,0]上递减.
,于是φ(x)在[-1,0]上递减. 依题意有

解得0≤m<

点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 的值为 .
的值为 .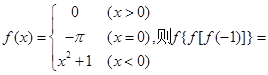
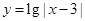 和
和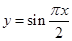
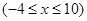 ,下列说法正确的是 .
,下列说法正确的是 .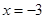 对称;
对称;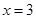 对称;
对称;
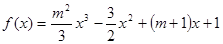
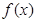 在
在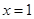 处取得极大值,求函数
处取得极大值,求函数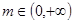 ,不等式
,不等式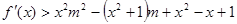 恒成立,求
恒成立,求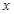 的取值范围
的取值范围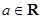 ,函数
,函数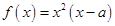 .
.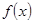 在区间
在区间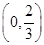 内是减函数,求实数
内是减函数,求实数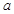 的取值范围;
的取值范围;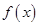 在区间
在区间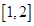 上的最小值
上的最小值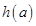 ;
; 在区间
在区间 上的最值.
上的最值. 和
和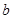 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: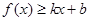 和
和 ,则称直线
,则称直线 为
为 ,
, 为自然对数的底数).
为自然对数的底数). 的极值;
的极值;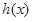 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.