题目内容
已知函数
(I)求函数 的最大值;
的最大值;
(Ⅱ)设 其中
其中 ,证明:
,证明:  <1.
<1.
解:(Ⅰ)
当 时,f(x)>0,f(x)单调递增;
时,f(x)>0,f(x)单调递增;
当 时,f(x)<0,f(x)单调递减.
时,f(x)<0,f(x)单调递减.
|
|
| 0 |
|
|
| + | 0 | - |
|
| ↗ | 极大值 | ↘ |
所以f(x)的最大值为f(0)=0.
(Ⅱ)由(Ⅰ)知,当 时,
时,
当 时,
时, 等价于
等价于
设 ,则
,则 .
.
当 时,
时, 则
则
从而当 时,
时, ,
, 在
在 单调递减.
单调递减.
当 时,
时,
即 ,
,
故g(x)<1.
综上,总有g(x)<1.

练习册系列答案
相关题目





 ,满足
,满足 的
的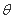 共有( )个
共有( )个 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有
,有 下面
下面 四个命题:其中正确命题序号是
四个命题:其中正确命题序号是 
 ②
② ③
③ ④
④ ⑤
⑤ 中,满足“对任意的
中,满足“对任意的 ,
,
 ,则
,则 恒成立”的函数是________.(填上所有正确的序号)
恒成立”的函数是________.(填上所有正确的序号) ,
, ,
, ,那么a等于
,那么a等于
 中,点
中,点 为底面
为底面 上的动点. 若三棱锥
上的动点. 若三棱锥 的表面积最大,则
的表面积最大,则 处
处 的中点处
的中点处 的中点处
的中点处 处
处 若实数x,y满足约束条件
若实数x,y满足约束条件 则
则 的最大值是
的最大值是 B.
B. C.
C. D.
D.