题目内容
已知函数![]()
(Ⅰ)若![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,且对于任意
,且对于任意![]() ,
,![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,求证:
,求证:![]()
解:(Ⅰ)由![]() 得
得![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,故
,故![]() 的单调递增区间是
的单调递增区间是![]() ,
,
由![]() 得
得![]() ,故
,故![]() 的单调递减区间是
的单调递减区间是![]() .
.
……………4分
(Ⅱ)解:由![]() 可知
可知![]() 是偶函数.
是偶函数.
于是![]() 对任意
对任意![]() 成立等价于
成立等价于![]() 对任意
对任意![]() 成立.
成立.
由![]() 得
得![]() .……………6
.……………6![]() 分
分
①当![]() 时,
时,![]() .
.
此时![]() 在
在![]() 上单调递增.
上单调递增.
故![]() ,符合题意.……………8分
,符合题意.……………8分
②当![]() 时,
时,![]() .
.
当![]() 变化时
变化时![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由此可得,在![]() 上,
上,![]() .
.
依题意,![]() ,又
,又![]() .
.
综合①,②得,实数![]() 的取值范围是
的取值范围是![]() .……………10分
.……………10分
(Ⅲ)
解![]() ,
,
![]()
![]() ,
,
……………11分
![]() ,
,
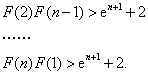 ……………12分
……………12分
由此得,![]() ……………13分
……………13分
故![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 ,
, 
 .
. , 函数
, 函数 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围; 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点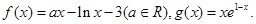
 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值; ,都有唯一的
,都有唯一的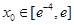 ,使得
,使得 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。
 ,求
,求 的单调递减区间;
的单调递减区间; ,求
,求 的最小值;
的最小值; ,且存在
,且存在 使得
使得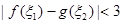 ,求实数
,求实数 的取值范围。
的取值范围。 .
. ,求函数
,求函数 在区间
在区间 的值域;
的值域; 上为增函数,求
上为增函数,求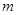 的取值范围.
的取值范围.