题目内容
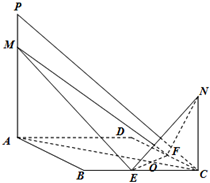 如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA、NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上一动点.
如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA、NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上一动点.(Ⅰ)求证:平面PAC⊥平面NEF;
(Ⅱ)若PC∥平面MEF,试求PM:MA的值.
分析:(Ⅰ)连结BD,通过证明EF⊥平面PAC,然后证明平面PAC⊥平面NEF;
(Ⅱ)法一:利用直线与平面平行,通过相似比直接推出PM:MA的值.
法二:建立如图所示的直角坐标系,推出点M为线段PA上靠近P的四等分点,得到结果.
(Ⅱ)法一:利用直线与平面平行,通过相似比直接推出PM:MA的值.
法二:建立如图所示的直角坐标系,推出点M为线段PA上靠近P的四等分点,得到结果.
解答: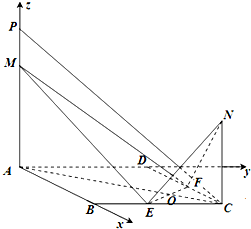 解:(Ⅰ)连结BD,
解:(Ⅰ)连结BD,
∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
又∵BD⊥AC,AC∩PA=A,∴BD⊥平面PAC,
又∵E,F分别是BC、CD的中点,∴EF∥BD,
∴EF⊥平面PAC,又EF?平面NEF,∴平面PAC⊥平面NEF;
(Ⅱ)法1:连结OM,∵PC∥平面MEF,平面PAC∩平面MEF=OM,∴PC∥OM,
∴
=
=
,故PM:MA=1:3
法2:建立如图所示的直角坐标系,则P(0,0,4),C(4,4,0),E(4,2,0),F(2,4,0),
∴
=(4,4,-4),
=(-2,2,0),
设点M的坐标为(0,0,m),平面MEF的法向量为
=(x,y,z),则
=(4,2,-m),
所以
,即
,
令x=1,则y=1,z=
,故
=(1,1,
),
∵PC∥平面MEF,∴
•
=0,即4+4-
=0,解得m=3,
故AM=3,即点M为线段PA上靠近P的四等分点;
故PM:MA=1:3
 解:(Ⅰ)连结BD,
解:(Ⅰ)连结BD,∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
又∵BD⊥AC,AC∩PA=A,∴BD⊥平面PAC,
又∵E,F分别是BC、CD的中点,∴EF∥BD,
∴EF⊥平面PAC,又EF?平面NEF,∴平面PAC⊥平面NEF;
(Ⅱ)法1:连结OM,∵PC∥平面MEF,平面PAC∩平面MEF=OM,∴PC∥OM,
∴
| PM |
| PA |
| OC |
| AC |
| 1 |
| 4 |
法2:建立如图所示的直角坐标系,则P(0,0,4),C(4,4,0),E(4,2,0),F(2,4,0),
∴
| PC |
| EF |
设点M的坐标为(0,0,m),平面MEF的法向量为
| n |
| ME |
所以
|
|
令x=1,则y=1,z=
| 6 |
| m |
| n |
| 6 |
| m |
∵PC∥平面MEF,∴
| PC |
| n |
| 24 |
| m |
故AM=3,即点M为线段PA上靠近P的四等分点;
故PM:MA=1:3
点评:本题考查平面与平面的垂直,直线与平面平行的性质定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目




 .
.