Question

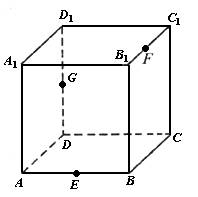
如图，已知E、F、G、H、K、L分别为正方体AC₁的棱AA₁、AB、BC、CC₁、C₁D₁、A₁D₁的中点.

求证：EF、GH、KL三线共面.

Answer 1

思路解析：利用向量法证明三直线共面即证明这三条直线的方向向量共面，即一个方向向量能用另外两个方向向量表示.

证明：设=a,=b,=c，则

==(-)=(a-c)，

===(b+c),

===-=- (a+b).

∴=--.

故EF、GH、KL三线共面.

方法归纳  选定基底后，想方设法地用基底表示所涉及到的元素，找到元素间满足的线性关系，从而证明三线共面.