题目内容
6.在区间[0,π]上随机取一个数x,使$-\frac{{\sqrt{3}}}{2}<cosx<\frac{{\sqrt{3}}}{2}$的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
分析 先求出不等式$-\frac{{\sqrt{3}}}{2}<cosx<\frac{{\sqrt{3}}}{2}$对应的解集,结合几何概型的概率公式进行求解即可.
解答 解:∵0≤x≤π,$-\frac{{\sqrt{3}}}{2}<cosx<\frac{{\sqrt{3}}}{2}$,
∴$\frac{π}{6}$≤x≤$\frac{5π}{6}$π,区间长度为$\frac{2}{3}π$,
则对应的概率P=$\frac{\frac{2}{3}π}{π}$=$\frac{2}{3}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,根据条件求出不等式等价条件是解决本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
16.已知函数y=|x-3|+1在区间[0,9]上的值域是( )
| A. | [4,7] | B. | [0,7] | C. | [1,7] | D. | [2,7] |
18.11月11日在某购物网站消费不超过10000元的2000名网购者中有女士1100名,男士900名.该网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析得到下表(消费金额:元)
女士消费情况:
男士消费情况:
(Ⅰ)计算x,y的值,在抽出的200名且消费金额在[8000,10000](单位:元)的网购者中随机选出2名发放网购红包,求选出的两名网购者都是男士的概率;
(Ⅱ)若消费金额不低于6000元的网购者为“网购达人”,低于6000元的网购者为“非网购达人”,根据以上数据填写下面2×2列连表,并回答能否在犯错误率不超过0.05的前提下,认为“是否为网购达人与性别有关”?
附:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$.
女士消费情况:
| 消费金额 | (0,2000) | [2000,4000) | [4000,6000) | [6000,8000) | [8000,10000] |
| 人数 | 10 | 25 | 35 | 35 | x |
| 消费金额 | (0,2000) | [2000,4000) | [4000,6000) | [6000,8000) | [8000,10000] |
| 人数 | 15 | 30 | 25 | y | 3 |
(Ⅱ)若消费金额不低于6000元的网购者为“网购达人”,低于6000元的网购者为“非网购达人”,根据以上数据填写下面2×2列连表,并回答能否在犯错误率不超过0.05的前提下,认为“是否为网购达人与性别有关”?
| 女士 | 男士 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
15.点M(1,1)到抛物线y=ax2准线的距离为3,则a的值为( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | $\frac{1}{8}或-\frac{1}{16}$ | D. | $\frac{1}{8}$或-16 |
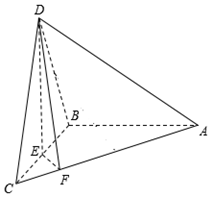 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,