题目内容
有一个受到污染的湖泊,其湖水的容积为v立方米,每天流出湖泊的水量都是r立方米.现假设下雨量和蒸发量正好平衡,且污染物质与湖水能很好地混合.用g(t)表示在t时刻每立方米湖水所含污染物质的克数,我们称之为在t时刻的湖水污染质量分数.已知目前污染源以每天p克的污染物质污染湖水,湖水污染质量分数满足关系式g(t)=![]() +[g(0)-
+[g(0)-![]() ]·e
]·e![]() (p≥0),其中g(0)是湖水污染的初始质量分数.
(p≥0),其中g(0)是湖水污染的初始质量分数.
(1)当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
(2)求证:当g(0)<![]() 时,该湖泊的污染程度会越来越严重;
时,该湖泊的污染程度会越来越严重;
(3)如果政府加大治污力度,使得该湖泊的所有污染源停止排放污染物,那么需要经过多少天才能使湖泊的污染程度下降到初始污染程度的5%?
答案:
解析:
解析:
(1)解:由g(t)为常数,得g(0)-![]() =0,所以g(0)=
=0,所以g(0)=![]() .
.
(2)证明:设0<t1<t2,则g(t1)-g(t2)
=![]() +
+![]() ·e
·e![]() -
-![]() -
-![]() ·e
·e![]()
=![]() ·
·
=![]() ·
· .
.
因为t1<t2,所以e![]() <e
<e![]() ,
,
所以e![]() -e
-e![]() >0.
>0.
又g(0)-![]() <0,所以g(t1)<g(t2).
<0,所以g(t1)<g(t2).
故湖水污染质量分数随时间的增加而增加,说明湖泊的污染程度会越来越严重.
(3)解:污染停止,即p=0,则g(t)=g(0)·e![]() .
.
设经过t天能使湖泊污染程度下降到初始污染程度的5%,即g(t)=5%·g(0),
所以![]() =e
=e![]() ,解得t=
,解得t=![]() ln20.
ln20.
故需要经过![]() ln20天才能使湖泊的污染程度下降到初始污染程度的5%.
ln20天才能使湖泊的污染程度下降到初始污染程度的5%.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
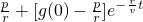 (p≥0),其中g(0)是湖水污染的初始质量分数.
(p≥0),其中g(0)是湖水污染的初始质量分数.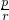 时,湖泊的污染程度将越来越严重;
时,湖泊的污染程度将越来越严重; (p≥0),其中g(0)是湖水污染的初始质量分数.
(p≥0),其中g(0)是湖水污染的初始质量分数.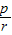 时,湖泊的污染程度将越来越严重;
时,湖泊的污染程度将越来越严重;