题目内容
已知变量x，y具有线性相关关系，测得（x，y）的一组数据如下：（0，1），（1，2），（2，4），（3，5），其回归方程为
，则a的值等于________．
0.9
分析：求出横标和纵标的平均数，写出样本中心点，把样本中心点代入线性回归方程，得到关于a的方程，解方程即可．
解答：∵
=
=1.5，
=
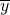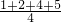=3，
∴这组数据的样本中心点是（1.5，3）
把样本中心点代入回归直线方程，
∴3=1.4×1.5+a，
∴a=0.9．
故答案为：0.9．
点评：本题考查线性回归方程，解题的关键是线性回归直线一定过样本中心点，这是求解线性回归方程的步骤之一．
分析：求出横标和纵标的平均数，写出样本中心点，把样本中心点代入线性回归方程，得到关于a的方程，解方程即可．
解答：∵
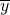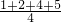==1.5，==3，∴这组数据的样本中心点是（1.5，3）
把样本中心点代入回归直线方程
，∴3=1.4×1.5+a，
∴a=0.9．
故答案为：0.9．
点评：本题考查线性回归方程，解题的关键是线性回归直线一定过样本中心点，这是求解线性回归方程的步骤之一．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
已知两个变量x和y之间具有线性相关系，5次试验的观测数据如下：
经计算得回归方程
=bx+a的系数b=0.575，则a等于（ ）
| x | 100 | 120 | 140 | 160 | 180 |
| y | 45 | 54 | 62 | 75 | 92 |
| ? |
| y |
| A、-14.9 | B、-13.9 |
| C、-12.9 | D、14.9 |
的系数b＝0.575，则a等于
的系数b＝0.575，则a等于已知两个变量x和y之间具有线性相关系，5次试验的观测数据如下：
| x | 100 | 120 | 140 | 160 | 180 |
| y | 45 | 54 | 62 | 75 | 92 |
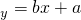的系数b=0.575，则a等于- A.-14.9
- B.-13.9
- C.-12.9
- D.14.9
已知两个变量x和y之间具有线性相关系，5次试验的观测数据如下：
经计算得回归方程
的系数b=0.575，则a等于（ ）
A．-14.9
B．-13.9
C．-12.9
D．14.9
| x | 100 | 120 | 140 | 160 | 180 |
| y | 45 | 54 | 62 | 75 | 92 |
的系数b=0.575，则a等于（ ）A．-14.9
B．-13.9
C．-12.9
D．14.9