题目内容
 如图,O是直角坐标原点,A、B是抛物线y2=2px(p>0)上异于顶点的两动点,且OA⊥OB,OM⊥AB并与AB相交于点M,求M点的轨迹方程.
如图,O是直角坐标原点,A、B是抛物线y2=2px(p>0)上异于顶点的两动点,且OA⊥OB,OM⊥AB并与AB相交于点M,求M点的轨迹方程.
解:根据条件,设点M,A,B的坐标分别为(x,y),(2pt12,2pt1),(2pt22,2pt2),t1≠t2,且t1t2≠0,
则 ,
, ,
,
 ,
,
∵ ,∴
,∴ ,
,
即(2pt1t2)2+(2p)2t1t2=0.
∴t1t2=-1.
∵ ,∴2px(t22-t12)+2py(t2-t1)=0,
,∴2px(t22-t12)+2py(t2-t1)=0,
∴ ,
,
∵ ,
, ,且A,M,B共线,
,且A,M,B共线,
∴(x-2pt12)(2pt2-y)=(y-2pt1)(2pt22-x),
化简得y(t1+t2)-2pt1t2-x=0,
由此可知M点的轨迹方程为x2+y2-2px=0,(x≠0).
分析:根据条件,设点M,A,B的坐标分别为(x,y),(2pt12,2pt1),(2pt22,2pt2),t1≠t2,且t1t2≠0,由题意知t1t2=-1. ,由此可知M点的轨迹方程.
,由此可知M点的轨迹方程.
点评:本题考查点的轨迹方程的求法,解题时要注意积累解题方法和解题技巧.
则
 ,
, ,
, ,
,∵
 ,∴
,∴ ,
,即(2pt1t2)2+(2p)2t1t2=0.
∴t1t2=-1.
∵
 ,∴2px(t22-t12)+2py(t2-t1)=0,
,∴2px(t22-t12)+2py(t2-t1)=0,∴
 ,
,∵
 ,
, ,且A,M,B共线,
,且A,M,B共线,∴(x-2pt12)(2pt2-y)=(y-2pt1)(2pt22-x),
化简得y(t1+t2)-2pt1t2-x=0,
由此可知M点的轨迹方程为x2+y2-2px=0,(x≠0).
分析:根据条件,设点M,A,B的坐标分别为(x,y),(2pt12,2pt1),(2pt22,2pt2),t1≠t2,且t1t2≠0,由题意知t1t2=-1.
 ,由此可知M点的轨迹方程.
,由此可知M点的轨迹方程.点评:本题考查点的轨迹方程的求法,解题时要注意积累解题方法和解题技巧.

练习册系列答案
相关题目
 如图,O是直角坐标原点,A、B是抛物线y2=2px(p>0)上异于顶点的两动点,且OA⊥OB,OM⊥AB并与AB相交于点M,求M点的轨迹方程.
如图,O是直角坐标原点,A、B是抛物线y2=2px(p>0)上异于顶点的两动点,且OA⊥OB,OM⊥AB并与AB相交于点M,求M点的轨迹方程.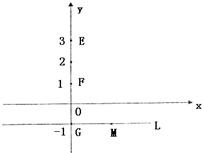 如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且
如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且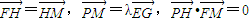 .
.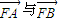 夹角为θ,且
夹角为θ,且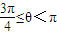 ,求直线m斜率的取值范围.
,求直线m斜率的取值范围.