题目内容
已知n=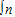
（2x+1）dx，数列{
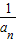}的前n项和为Sn，数列{bn}的通项公式为bn=n-35，n∈N*，则bnSn的最小值为 ．
【答案】分析：由题意，先由微积分基本定理求出an再根据通项的结构求出数列{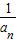 
}的前n项和为Sn，然后代入求bnSn的最小值即可得到答案
解答：解：an=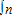
（2x+1）dx=（x2+x） 
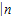=n2+n
∴
=
=
-
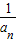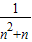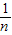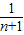
∴数列{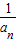
}的前n项和为Sn=
+
+…+
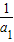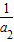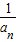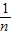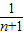=1-
+
-
+…+
-
=1-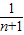
=
，
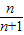bn=n-35，n∈N*，
则bnSn=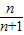
×（n-35）=n+1+
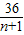-37≥2×6-37=-25，
等号当且仅当n+1=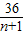
，即n=5时成立，
故bnSn的最小值为-25．
故答案为：-25
点评：本题考查微积分基本定理及数列的求和，数列的最值等问题，综合性强，知识转换快，解题时要严谨认真，莫因变形出现失误导致解题失败．
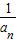}的前n项和为Sn，然后代入求bnSn的最小值即可得到答案解答：解：an=
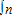（2x+1）dx=（x2+x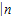） =n2+n∴
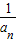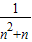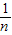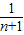
==-∴数列{
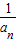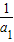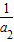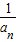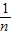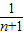}的前n项和为Sn=++…+=1-+-+…+-=1-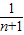=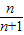，bn=n-35，n∈N*，
则bnSn=
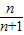×（n-35）=n+1+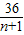-37≥2×6-37=-25，等号当且仅当n+1=
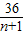，即n=5时成立，故bnSn的最小值为-25．
故答案为：-25
点评：本题考查微积分基本定理及数列的求和，数列的最值等问题，综合性强，知识转换快，解题时要严谨认真，莫因变形出现失误导致解题失败．
练习册系列答案
相关题目
（2x+1）dx，数列{
}的前n项和为Sn，bn=n-33，n∈N*，则bnSn的最小值为 ．
（2x+1）dx，数列{
}的前n项和为Sn，bn=n-33，n∈N*，则bnSn的最小值为 ．