题目内容
在平面直角坐标系中，若不等式组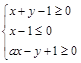
（
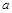为常数）所表示的平面区域内的面积等于2，则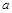的值为（ ）
| A．-5 | B．1 | C．2 | D．3 |
D
解析试题分析：作图可知可行域为三角形，三个顶点为
，由面积为2得
考点：线性规划问题
点评：线性规划问题常考的题型还有求目标函数最值
练习册系列答案
天天向上一本好卷系列答案
相关题目
的取值范围是
已知变量x，y满足约束条件
，则z=3|x|+y的取值范围为（ ）
| A．[-1,5] | B．[1, 11] | C．[5, 11] | D．[-7, 11] |
已知平面区域如右图所示，
在平面区域内取得最大值的最优解有无数多个，则
的值为 （ ）
A． | B． | C． | D．不存在 |
已知正三角形ABC的顶点A(1,1)，B(1,3)，顶点C在第一象限，若点（x，y）在△ABC内部，则
的取值范围是( )
A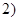． ， | B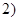． ， | C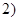． ， | D．， |
已知点
，则
的最大值为( )
A． | B． | C． | D． |
点(3,1)和(－4,6)在直线3x－2y＋a＝0的两侧，则( )
| A．a＜－7或a＞24 | B．－7＜a＜24 |
| C．a＝－7或a＝24 | D．以上都不对 |
如果实数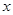
、
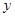满足条件
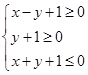，那么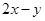
的最大值为（ ）
A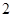． | B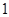． | C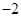． | D． |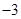
实数
满足不等式组
，那么目标函数
的最小值是 （ ）
| A．-15 | B．-6 | C．-5 | D．-2 |