题目内容

在数列{a_n}中，S_n为其前n项之和，且S_n=2ⁿ-1，则a₁²+a₂²+a₃²+…+a_n²等于：

A.
（2ⁿ-1）²
B.
$数学公式$
C.
4ⁿ-1
D.
$数学公式$

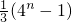
D
分析：首先根据前n项和S_n=2ⁿ-1，解出数列a_n通项，在平方，观察到是等比数列，再根据等比数列的前n项和的公式求解．
解答：因为a_n=S_n-S_n-1，又S_n=2ⁿ-1
所以a_n=2ⁿ-2^n-1=2^n-1所以，a_n²=4^n-1是等比数列
设A_n=a₁²+a₂²+a₃²+…+a_n²
由等比数列前n项和 $\text{[math]}$ ，q=4
解得 $\text{[math]}$
所以答案为D
点评：此题主要考查数列的求和问题，其中应用到由前n项和求数列通项和等比数列的前n项和公式，这些都需要理解并记忆．

练习册系列答案

夺冠百分百中考试题调研系列答案

新阅读训练营系列答案

口算题卡每天100道系列答案

中考夺标最新模拟试题系列答案

分层课课练系列答案

创新成功学习名校密卷系列答案

名师点拨课时作业甘肃教育出版社系列答案

小学奥数举一反三系列答案

新课标初中单元测试卷系列答案

口算应用一卡通系列答案

相关题目

如果由数列{a_n}生成的数列{b_n}满足对任意的n∈N^*均有b_n+1＜b_n，其中b_n=a_n+1-a_n，则称数列{a_n}为“Z数列”．
（Ⅰ）在数列{a_n}中，已知a_n=-n²，试判断数列{a_n}是否为“Z数列”；
（Ⅱ）若数列{a_n}是“Z数列”，a₁=0，b_n=-n，求a_n；
（Ⅲ）若数列{a_n}是“Z数列”，设s，t，m∈N^*，且s＜t，求证：a_t+m-a_s+m＜a_t-a_s．

（1）若对于任意的n∈N^*，总有

成立，求常数A，B的值；
（2）在数列{a_n}中，a1=

（n≥2，n∈N^*），求通项a_n；
（3）在（2）题的条件下，设bn=

，从数列{b_n}中依次取出第k₁项，第k₂项，…第k_n项，按原来的顺序组成新的数列{c_n}，其中cn=bkn，其中k₁=m，k_n+1-k_n=r∈N^*．试问是否存在正整数m，r使

(c1+c2+…+cn)=S且

成立？若存在，求正整数m，r的值；不存在，说明理由．

下列几种推理过程是演绎推理的是（　　）

A．某校高三1班55人，2班54人，3班52人，由此得高三所有班级的人数超过50人

B．由圆的周长C=πd推测球的表面积S=πd²

C．两条直线平行，同旁内角互补，如果∠A与∠B是两条平行直线的同旁内角，则∠A+∠B=180°

D．在数列{a_n}中，a₁=1，a_n=

）（n≥2），由此归纳数列{a_n}的通项公式

记公差d≠0的等差数列{a_n}的前n项和为S_n，已知a₁=2+

．
（1）求数列{a_n}的通项公式a_n及前n项和S_n；
（2）记b_n=a_n-

，若自然数n₁，n₂，…，n_k，…满足1≤n₁＜n₂＜…＜n_k＜…，并且b n1，b n2，…，b nk，…成等比数列，其中n₁=1，n₂=3，求n_k（用k表示）；
（3）试问：在数列{a_n}中是否存在三项a_r，a_s，a_t（r＜s＜t，r，s，t∈N^*）恰好成等比数列？若存在，求出此三项；若不存在，请说明理由．

(本小题满分16分)记公差d≠0的等差数列{a_n}的前n项和为S_n，已知a₁＝2＋，S₃＝12＋．

（1）求数列{a_n}的通项公式a_n及前n项和S_n；

（2）记b_n＝a_n－，若自然数n₁，n₂，…，n_k，…满足1≤n₁＜n₂＜…＜n_k＜…，并且，，…，，…成等比数列，其中n₁＝1，n₂＝3，求n_k（用k表示）；

（3）试问：在数列{a_n}中是否存在三项a_r，a_s，a_t(r＜s＜t，r，s，t∈N*)恰好成等比数列？若存在，求出此三项；若不存在，请说明理由．