题目内容
(本小题满分13分)
已知函数 、
、
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若 为正常数,设
为正常数,设 ,求函数
,求函数 的最小值;
的最小值;
(Ⅲ)若 ,
, ,证明:
,证明: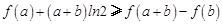 、
、
已知函数
 、
、(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若
 为正常数,设
为正常数,设 ,求函数
,求函数 的最小值;
的最小值;(Ⅲ)若
 ,
, ,证明:
,证明: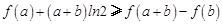 、
、(Ⅰ)∵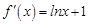 ,解
,解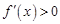 ,得
,得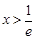 ;解
;解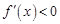 ,得
,得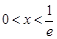 .
.
∴ 的单调递增区间是
的单调递增区间是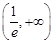 ,单调递减区间是
,单调递减区间是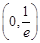 . ……3′
. ……3′
(Ⅱ)∵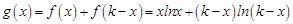 ,定义域是
,定义域是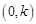 .
.
∴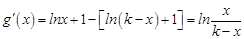 ……5′
……5′
由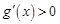 ,得
,得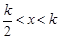 ,由
,由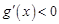 ,得
,得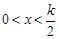
∴ 函数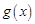 在
在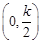 上单调递减;在
上单调递减;在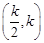 上单调递增……7′
上单调递增……7′
故函数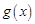 的最小值是:
的最小值是: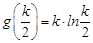 . ……8′
. ……8′
(Ⅲ)∵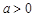 ,
, ,∴ 在(Ⅱ)中取
,∴ 在(Ⅱ)中取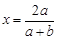 ,
,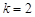


 可得
可得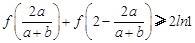 ,即
,即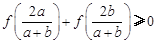 .……10′
.……10′
∴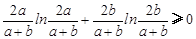 ,∴
,∴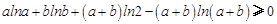 .
.
即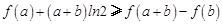 .……12′
.……12′
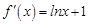 ,解
,解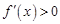 ,得
,得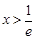 ;解
;解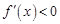 ,得
,得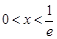 .
.∴
 的单调递增区间是
的单调递增区间是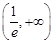 ,单调递减区间是
,单调递减区间是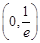 . ……3′
. ……3′(Ⅱ)∵
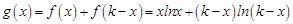 ,定义域是
,定义域是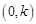 .
.∴
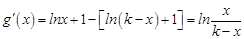 ……5′
……5′由
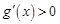 ,得
,得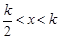 ,由
,由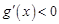 ,得
,得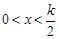
∴ 函数
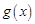 在
在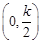 上单调递减;在
上单调递减;在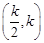 上单调递增……7′
上单调递增……7′故函数
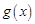 的最小值是:
的最小值是: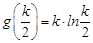 . ……8′
. ……8′(Ⅲ)∵
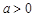 ,
, ,∴ 在(Ⅱ)中取
,∴ 在(Ⅱ)中取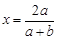 ,
,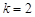


 可得
可得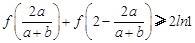 ,即
,即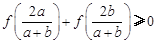 .……10′
.……10′∴
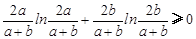 ,∴
,∴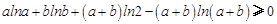 .
.即
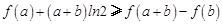 .……12′
.……12′略

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 为定义在
为定义在 上的可导函数,且
上的可导函数,且 对于
对于 恒成立且e为自然对数的底,则
恒成立且e为自然对数的底,则 与
与 的大小关系是
的大小关系是 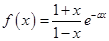

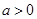 ,讨论
,讨论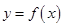 的单调性;
的单调性;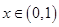 恒有
恒有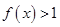 ,求
,求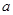 的取值范围
的取值范围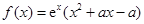 ,其中
,其中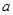 是常数.
是常数.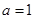 时,求
时,求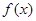 在点
在点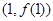 处的切线方程;
处的切线方程;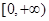 上的最小值.
上的最小值.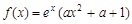
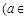 R).
R).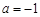 ,求曲线
,求曲线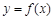 在点
在点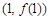 处的的切线方程;
处的的切线方程; 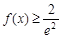 对任意
对任意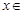
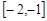 恒成立,求实数
恒成立,求实数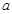 的取值范围.
的取值范围.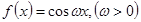 将
将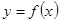 的图象向右平移
的图象向右平移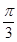 个单位长
个单位长 的最小值等于( )
的最小值等于( )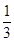
 的图象与直线
的图象与直线 相切,则a等于( )
相切,则a等于( )


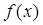 是偶函数,当
是偶函数,当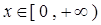 时,
时,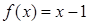 ,则
,则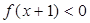 解集为:
解集为: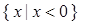




 在点
在点 处的切线与直线
处的切线与直线 垂直,求a的值;
垂直,求a的值; 单调递增,求a的取值范围;
单调递增,求a的取值范围; 1<a<3,证明:对任意
1<a<3,证明:对任意 都有
都有 >1成立.
>1成立.