Question

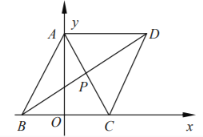
【题目】如图，在平行四边形中，点，，，对角线，交于点P.

（1）求直线的方程；

（2）若点E，F分别在平行四边形的边和上运动，且，求的取值范围；

（3）试写出三角形区域（包括边界）所满足的线性约束条件，若在该区域上任取一点M，使，试求的取值范围.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）设，根据利用坐标运算求出点坐标，进而可求出直线的方程；

（2）设，则，，利用向量的线性运算将用表示出来，利用二次函数的性质求出取值范围；

（3）通过直线的方程，可得三角形区域（包括边界）所满足的线性约束条件，设，利用将用表示出来，利用线性规划的知识可求出的取值范围.

解：（1）设，

则，

又，且，

，

，

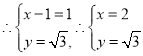所以直线的方程为：，

即；

（2）设，则，，

，

由（1）得直线的方程为，

所以，

，

，

；

（3），即，

，即，

所以三角形区域（包括边界）所满足的线性约束条件为：

，

设，

则，

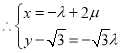，整理可得，

令，则

当取点时，取最大值，即，

当取点时，取最小值，即，

所以的取值范围是.