题目内容
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)若对于![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 在
在![]() 处取得极大值为
处取得极大值为![]() ,无极小值.(Ⅱ)
,无极小值.(Ⅱ)![]()
【解析】
(Ⅰ)求得f(x)的导数,可得切线的斜率,由两直线平行的条件:斜率相等,可得a,求出f(x)的导数和单调区间,即可得到所求极值;
(Ⅱ)设x1>x2,可得f(x1)﹣f(x2)>mx12﹣mx22,设g(x)=f(x)﹣mx2在(0,+∞)为增函数,设g(x)=f(x)﹣mx2在(0,+∞)为增函数,求得g(x)的导数,再由参数分离和构造函数,求出最值,即可得到所求m的范围.
(Ⅰ)![]() 的导数为
的导数为![]() ,
,
可得![]() 的图象在点
的图象在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
由切线与直线![]() 平行,可得
平行,可得![]() ,即
,即![]() ,
,
![]() ,
,![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时, ,
时, ,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
可得![]() 在
在![]() 处取得极大值为
处取得极大值为![]() ,无极小值.
,无极小值.
(Ⅱ)设![]() ,若
,若![]() ,可得
,可得![]() ,
,
即![]()
设![]() 在
在![]() 上增函数,
上增函数,
即![]() 在
在![]() 上恒成立,
上恒成立,
可得![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,![]() 在
在![]() 处取得极小值为
处取得极小值为![]() ,
,
所以![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船一天的捕鱼量的平均数;
的渔船一天的捕鱼量的平均数;
(Ⅱ)若以(Ⅰ)中确定的平均数作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①估计一艘上述吨位的捕鱼船一年在捕鱼期内的捕鱼总量;
②已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘;若不捕鱼,每天成本为2万元/艘,请依据往年天气统计数据,估计一艘此种捕鱼船年利润不少于1600万元的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
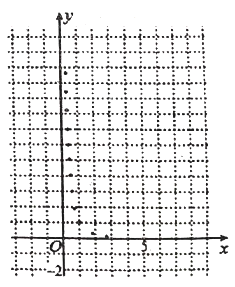
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为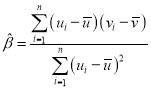 ,
,![]()