题目内容
设数列{an}是等差数列,a5=6.
(1)当a3=3时,请在数列{an}中找一项am,使得a3,a5,am成等比数列;
(2)当a3=2时,若自然数n1,n2,…,nt,… (t∈N*)满足5<n1<n2<…<nt<…使得a3,a5,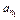 ,
,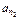 ,…,
,…,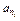 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.
(1)当a3=3时,请在数列{an}中找一项am,使得a3,a5,am成等比数列;
(2)当a3=2时,若自然数n1,n2,…,nt,… (t∈N*)满足5<n1<n2<…<nt<…使得a3,a5,
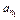 ,
,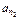 ,…,
,…,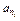 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.(1)a3,a5,a9成等比数列(2)n =3t+1+2,t=1,2,3,….
=3t+1+2,t=1,2,3,….
 =3t+1+2,t=1,2,3,….
=3t+1+2,t=1,2,3,….(1)设{an}的公差为d,则由a5=a3+2d,
得d= =
= ,由ama3=a
,由ama3=a ,即3
,即3 =62,解得m=9.即a3,a5,a9成等比数列.
=62,解得m=9.即a3,a5,a9成等比数列.
(2)∵a3=2,a5=6,∴d= =2,∴当n≥5时,an=a5+(n-5)d=2n-4,
=2,∴当n≥5时,an=a5+(n-5)d=2n-4,
又a3,a5,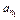 ,
,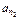 ,…,
,…,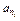 ,…成等比数列,
,…成等比数列,
则q= =
= =3,
=3,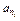 =a5·3t,t=1,2,3,….
=a5·3t,t=1,2,3,….
又an =2n
=2n -4,∴2n
-4,∴2n -4=a5·3t=6·3t,
-4=a5·3t=6·3t,
∴2n =2·3t+1+4.
=2·3t+1+4.
即n =3t+1+2,t=1,2,3,….
=3t+1+2,t=1,2,3,….
得d=
 =
= ,由ama3=a
,由ama3=a ,即3
,即3 =62,解得m=9.即a3,a5,a9成等比数列.
=62,解得m=9.即a3,a5,a9成等比数列.(2)∵a3=2,a5=6,∴d=
 =2,∴当n≥5时,an=a5+(n-5)d=2n-4,
=2,∴当n≥5时,an=a5+(n-5)d=2n-4,又a3,a5,
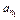 ,
,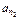 ,…,
,…,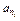 ,…成等比数列,
,…成等比数列,则q=
 =
= =3,
=3,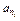 =a5·3t,t=1,2,3,….
=a5·3t,t=1,2,3,…. 又an
 =2n
=2n -4,∴2n
-4,∴2n -4=a5·3t=6·3t,
-4=a5·3t=6·3t,∴2n
 =2·3t+1+4.
=2·3t+1+4.即n
 =3t+1+2,t=1,2,3,….
=3t+1+2,t=1,2,3,….
练习册系列答案
相关题目

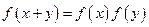
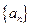 满足
满足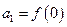 ,且
,且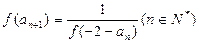 ,数列
,数列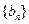 满足
满足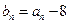
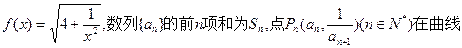
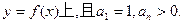
 }的通项公式
}的通项公式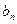 }的首项b1=1,前n项和为Tn,且
}的首项b1=1,前n项和为Tn,且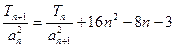 ,求数列{
,求数列{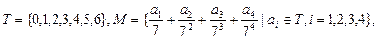 将M中的元素按从大到小的顺序排列,则第2005个数是( )
将M中的元素按从大到小的顺序排列,则第2005个数是( )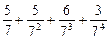
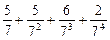
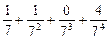
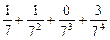
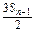 总成等差数列.
总成等差数列.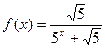 ,
,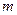 为正整数.
为正整数.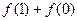 和
和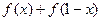 的值;
的值;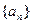 的通项公式为
的通项公式为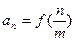 (
(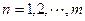 ),求数列
),求数列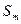 ;
;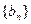 满足:
满足: ,
,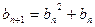 ,设
,设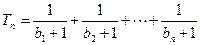 ,若(Ⅱ)中的
,若(Ⅱ)中的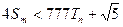 恒成立,试求m的最大值.
恒成立,试求m的最大值.